Chapter 6 Case study: interface design
This chapter presents a case study that demonstrates a process for designing functions that work together.
It introduces the turtle module, which allows you to create images using turtle graphics. The turtle module is included in most Python installations, but if you are running Python using PythonAnywhere, you won’t be able to run the turtle examples (at least you couldn’t when I wrote this).
6.1 The turtle module
To check whether you have the turtle module, open the Python interpreter and type
When you run this code, it should create a new window with small arrow that represents the turtle. Close the window.
Create a file named mypolygon.py and type in the following code:
The turtle module (with a lowercase ’t’) provides a function called Turtle (with an uppercase ’T’) that creates a Turtle object, which we assign to a variable named bob. Printing bob displays something like:
This means that bob refers to an object with type Turtle as defined in module turtle.
mainloop tells the window to wait for the user
to do something, although in this case there’s not much for
the user to do except close the window.
Once you create a Turtle, you can call a method to move it around the window. A method is similar to a function, but it uses slightly different syntax. For example, to move the turtle forward:
The method, fd, is associated with the turtle object we’re calling bob. Calling a method is like making a request: you are asking bob to move forward.
The argument of fd is a distance in pixels, so the actual size depends on your display.
Other methods you can call on a Turtle are bk to move backward, lt for left turn, and rt right turn. The argument for lt and rt is an angle in degrees.
Also, each Turtle is holding a pen, which is either down or up; if the pen is down, the Turtle leaves a trail when it moves. The methods pu and pd stand for “pen up” and “pen down”.
To draw a right angle, add these lines to the program
(after creating bob and before calling mainloop):
When you run this program, you should see bob move east and then north, leaving two line segments behind.
Now modify the program to draw a square. Don’t go on until you’ve got it working!
6.2 Simple repetition
Chances are you wrote something like this:
We can do the same thing more concisely with a for statement. Add this example to mypolygon.py and run it again:
You should see something like this:
This is the simplest use of the for statement; we will see more later. But that should be enough to let you rewrite your square-drawing program. Don’t go on until you do.
Here is a for statement that draws a square:
The syntax of a for statement is similar to a function definition. It has a header that ends with a colon and an indented body. The body can contain any number of statements.
A for statement is also called a loop because the flow of execution runs through the body and then loops back to the top. In this case, it runs the body four times.
This version is actually a little different from the previous square-drawing code because it makes another turn after drawing the last side of the square. The extra turn takes more time, but it simplifies the code if we do the same thing every time through the loop. This version also has the effect of leaving the turtle back in the starting position, facing in the starting direction.
6.3 Exercises
The following is a series of exercises using the turtle module. They are meant to be fun, but they have a point, too. While you are working on them, think about what the point is.
The following sections have solutions to the exercises, so don’t look until you have finished (or at least tried).
-
1.
Write a function called square that takes a parameter named t, which is a turtle. It should use the turtle to draw a square.
Write a function call that passes bob as an argument to square, and then run the program again.
-
2.
Add another parameter, named length, to square. Modify the body so length of the sides is length, and then modify the function call to provide a second argument. Run the program again. Test your program with a range of values for length.
-
3.
Make a copy of square and change the name to polygon. Add another parameter named n and modify the body so it draws an n-sided regular polygon. Hint: The exterior angles of an n-sided regular polygon are degrees.
-
4.
Write a function called circle that takes a turtle, t, and radius, r, as parameters and that draws an approximate circle by calling polygon with an appropriate length and number of sides. Test your function with a range of values of r.
Hint: figure out the circumference of the circle and make sure that length * n = circumference.
-
5.
Make a more general version of circle called arc that takes an additional parameter angle, which determines what fraction of a circle to draw. angle is in units of degrees, so when angle=360, arc should draw a complete circle.
6.4 Encapsulation
The first exercise asks you to put your square-drawing code into a function definition and then call the function, passing the turtle as a parameter. Here is a solution:
The innermost statements, fd and lt are indented twice to show that they are inside the for loop, which is inside the function definition. The next line, square(bob), is flush with the left margin, which indicates the end of both the for loop and the function definition.
Inside the function, t refers to the same turtle bob, so t.lt(90) has the same effect as bob.lt(90). In that case, why not call the parameter bob? The idea is that t can be any turtle, not just bob, so you could create a second turtle and pass it as an argument to square:
Wrapping a piece of code up in a function is called encapsulation. One of the benefits of encapsulation is that it attaches a name to the code, which serves as a kind of documentation. Another advantage is that if you re-use the code, it is more concise to call a function twice than to copy and paste the body!
6.5 Generalization
The next step is to add a length parameter to square. Here is a solution:
Adding a parameter to a function is called generalization because it makes the function more general: in the previous version, the square is always the same size; in this version it can be any size.
The next step is also a generalization. Instead of drawing squares, polygon draws regular polygons with any number of sides. Here is a solution:
This example draws a 7-sided polygon with side length 70.
When a function has more than a few numeric arguments, it is easy to forget what they are, or what order they should be in. In that case it is often a good idea to include the names of the parameters in the argument list:
These are called keyword arguments because they include the parameter names as “keywords” (not to be confused with Python keywords like while and def).
This syntax makes the program more readable. It is also a reminder about how arguments and parameters work: when you call a function, the arguments are assigned to the parameters.
6.6 Interface design
The next step is to write circle, which takes a radius, r, as a parameter. Here is a simple solution that uses polygon to draw a 50-sided polygon:
The first line computes the circumference of a circle with radius r using the formula . Since we use math.pi, we have to import math. By convention, import statements are usually at the beginning of the script.
n is the number of line segments in our approximation of a circle, so length is the length of each segment. Thus, polygon draws a 50-sided polygon that approximates a circle with radius r.
One limitation of this solution is that n is a constant, which means that for very big circles, the line segments are too long, and for small circles, we waste time drawing very small segments. One solution would be to generalize the function by taking n as a parameter. This would give the user (whoever calls circle) more control, but the interface would be less clean.
The interface of a function is a summary of how it is used: what are the parameters? What does the function do? And what is the return value? An interface is “clean” if it allows the caller to do what they want without dealing with unnecessary details.
In this example, r belongs in the interface because it specifies the circle to be drawn. n is less appropriate because it pertains to the details of how the circle should be rendered.
Rather than clutter up the interface, it is better to choose an appropriate value of n depending on circumference:
Now the number of segments is an integer near circumference/3, so the length of each segment is approximately 3, which is small enough that the circles look good, but big enough to be efficient, and acceptable for any size circle.
Adding 3 to n guarantees that the polygon has at least 3 sides.
6.7 Refactoring
When I wrote circle, I was able to re-use polygon because a many-sided polygon is a good approximation of a circle. But arc is not as cooperative; we can’t use polygon or circle to draw an arc.
One alternative is to start with a copy of polygon and transform it into arc. The result might look like this:
The second half of this function looks like polygon, but we can’t re-use polygon without changing the interface. We could generalize polygon to take an angle as a third argument, but then polygon would no longer be an appropriate name! Instead, let’s call the more general function polyline:
Now we can rewrite polygon and arc to use polyline:
Finally, we can rewrite circle to use arc:
This process—rearranging a program to improve interfaces and facilitate code re-use—is called refactoring. In this case, we noticed that there was similar code in arc and polygon, so we “factored it out” into polyline.
If we had planned ahead, we might have written polyline first and avoided refactoring, but often you don’t know enough at the beginning of a project to design all the interfaces. Once you start coding, you understand the problem better. Sometimes refactoring is a sign that you have learned something.
6.8 A development plan
A development plan is a process for writing programs. The process we used in this case study is “encapsulation and generalization”. The steps of this process are:
-
1.
Start by writing a small program with no function definitions.
-
2.
Once you get the program working, identify a coherent piece of it, encapsulate the piece in a function and give it a name.
-
3.
Generalize the function by adding appropriate parameters.
-
4.
Repeat steps 1–3 until you have a set of working functions. Copy and paste working code to avoid retyping (and re-debugging).
-
5.
Look for opportunities to improve the program by refactoring. For example, if you have similar code in several places, consider factoring it into an appropriately general function.
This process has some drawbacks—we will see alternatives later—but it can be useful if you don’t know ahead of time how to divide the program into functions. This approach lets you design as you go along.
6.9 docstring
A docstring is a string at the beginning of a function that explains the interface (“doc” is short for “documentation”). Here is an example:
By convention, all docstrings are triple-quoted strings, also known as multiline strings because the triple quotes allow the string to span more than one line.
It is terse, but it contains the essential information someone would need to use this function. It explains concisely what the function does (without getting into the details of how it does it). It explains what effect each parameter has on the behavior of the function and what type each parameter should be (if it is not obvious).
Writing this kind of documentation is an important part of interface design. A well-designed interface should be simple to explain; if you have a hard time explaining one of your functions, maybe the interface could be improved.
6.10 Debugging
An interface is like a contract between a function and a caller. The caller agrees to provide certain parameters and the function agrees to do certain work.
For example, polyline requires four arguments: t has to be a Turtle; n has to be an integer; length should be a positive number; and angle has to be a number, which is understood to be in degrees.
These requirements are called preconditions because they are supposed to be true before the function starts executing. Conversely, conditions at the end of the function are postconditions. Postconditions include the intended effect of the function (like drawing line segments) and any side effects (like moving the Turtle or making other changes).
Preconditions are the responsibility of the caller. If the caller violates a (properly documented!) precondition and the function doesn’t work correctly, the bug is in the caller, not the function.
If the preconditions are satisfied and the postconditions are not, the bug is in the function. If your pre- and postconditions are clear, they can help with debugging.
6.11 Glossary
- method:
-
A function that is associated with an object and called using dot notation.
- loop:
-
A part of a program that can run repeatedly.
- encapsulation:
-
The process of transforming a sequence of statements into a function definition.
- generalization:
-
The process of replacing something unnecessarily specific (like a number) with something appropriately general (like a variable or parameter).
- keyword argument:
-
An argument that includes the name of the parameter as a “keyword”.
- interface:
-
A description of how to use a function, including the name and descriptions of the arguments and return value.
- refactoring:
-
The process of modifying a working program to improve function interfaces and other qualities of the code.
- development plan:
-
A process for writing programs.
- docstring:
-
A string that appears at the top of a function definition to document the function’s interface.
- precondition:
-
A requirement that should be satisfied by the caller before a function starts.
- postcondition:
-
A requirement that should be satisfied by the function before it ends.
6.12 Exercises
Exercise 6.1.
-
1.
Draw a stack diagram that shows the state of the program while executing circle(bob, radius). You can do the arithmetic by hand or add print statements to the code.
-
2.
The version of arc in Section 6.7 is not very accurate because the linear approximation of the circle is always outside the true circle. As a result, the Turtle ends up a few pixels away from the correct destination. My solution shows a way to reduce the effect of this error. Read the code and see if it makes sense to you. If you draw a diagram, you might see how it works.
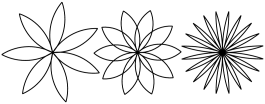
Exercise 6.2.
Write an appropriately general set of functions that can draw flowers as in Figure 6.1.
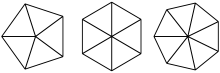
Exercise 6.3.
Write an appropriately general set of functions that can draw shapes as in Figure 6.2.
Exercise 6.4.
Read about spirals at http://en.wikipedia.org/wiki/Spiral; then write a program that draws an Archimedian spiral (or one of the other kinds).