Boolean Expressions
In CS131 you worked with simple Boolean expressions —
expressions that return a true or false
value. An example is
if (this.isBesideThing())
{ this.pickThing();
}
This code could be from a new Robot class. It
only picks up a Thing if the Boolean expression
this.isBesideThing() returns true
— that is, the robot is beside a Thing.
Just as arithmetic expressions can be combined, so can Boolean
expressions. Recall the addition table from grade 2 math. It
shows how to combine integers using the plus operation:
| + |
0 |
1 |
2 |
3 |
| 0 |
0 |
1 |
2 |
3 |
| 1 |
1 |
2 |
3 |
4 |
| 2 |
2 |
3 |
4 |
5 |
| 3 |
3 |
4 |
5 |
6 |
We can form a similar tables for combining Boolean
expressions with the OR (|| in Java) and AND
(&&) operations:
|| |
true |
false |
true |
true |
true |
false |
true |
false |
|
&& |
true |
false |
true |
true |
false |
false |
false |
false |
|
Tables are often helpful for convincing yourself that a
Boolean expression is correct. For example, you might decide to
watch television tonight if the homework due tomorrow is finished
and all your remaining homework is due after the weekend or your
“special friend” is visiting. Expressing this as a Java
predicate looks like:
public boolean watchTV(boolean tomorrowDone, boolean restNotDue, boolean visitor)
{ if (tomorrowDone && restNotDue || visitor)
{ return true;
} else
{ return false;
}
}
A truth table can be constructed for this problem with the
following steps:
- Construct an expression tree for the Boolean expression. This
is like an arithmetic expression tree, as shown in Section 7.1.1
of the Robots textbook. The order of operations is:
- Subexpressions grouped with parentheses
- Negation (not)
- And
- Or
The expression given above would be:
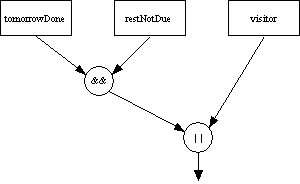
- Make a table with one column for each variable in the
expression tree plus one column for each Boolean operator in the
expression. In the following, the first row is for clarity only
(so you can see a picture of what we're talking about), the second
row is used to number the columns, and the thrid row
contains the variables and Boolean operators as described above.
Normally you would only write the second and third rows.
 |
 |
 |
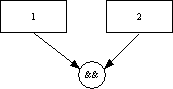 |
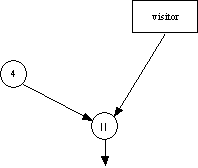 |
| 1 |
2 |
3 |
4 |
5 |
tomorrowDone |
restNotDue |
visitor |
1 && 2 |
4 || 3 |
- Count the number of variables in the expression. Raise 2 to
that number, in this case 23 or 8. Add that many rows.
- Alternate
true and false in the
first column. Alternate pairs of true and
false in the second column. Alternate groups of four
trues and four falses in the third
column. This pattern can be extended for any number of boolean
variables. Notice the pattern in the colours in the table,
below.
- Finally, compute the value for the remaining columns, using
the truth tables introduced at the beginning of the lab. The last
column shows that there are only three combinations of the
variables where you would choose not to watch television.
tomorrowDone |
restNotDue |
visitor |
1 && 2 |
4 || visitor |
| true |
true |
true |
true |
true |
| false |
true |
true |
false |
true |
| true |
false |
true |
false |
true |
| false |
false |
true |
false |
true |
| true |
true |
false |
true |
true |
| false |
true |
false |
false |
false |
| true |
false |
false |
false |
false |
| false |
false |
false |
false |
false |
Suppose that there was an additional Boolean variable,
scaredOfFailing and that the Boolean expression was
if ((tomorrowDone && restNotDue || visitor) && !scaredOfFailing)
How many rows would you ADD to the table, above?


