CS 488/688: Introduction to Computer Graphics

Assignment 2: Pipeline

Summary

Your goal of this assignment is to write a program to draw a wireframe cube:

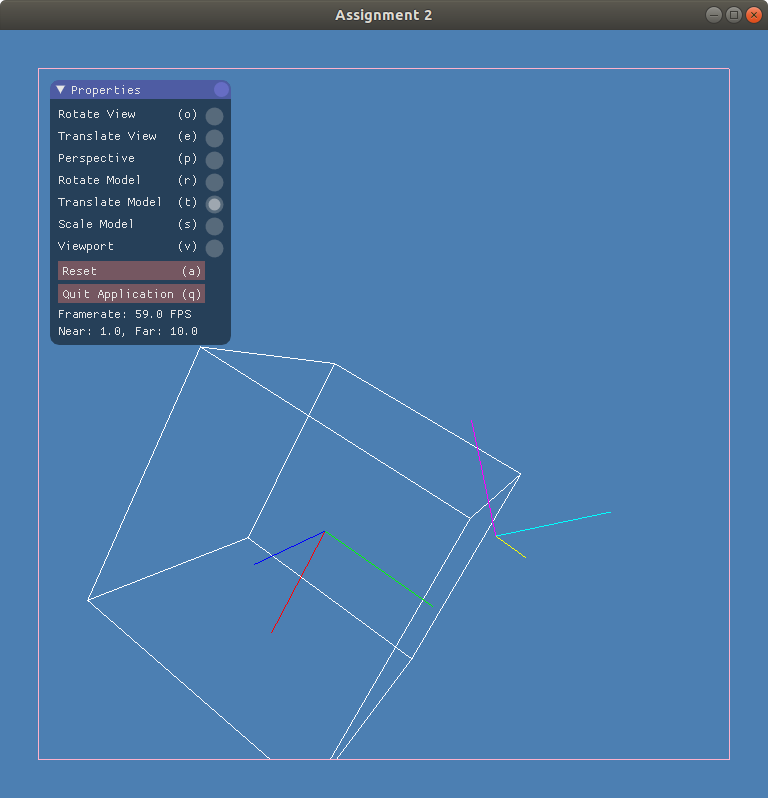
You can apply modelling transformations to the cube, and viewing transformations to the camera. Well, that might sound all too easy, especially in light of all the cubes in Assignment 1, but there's a catch: all you're allowed to do is draw lines directly in normalized device coordinates. You will be responsible for implementing the geometric pipeline, including perspective projection and clipping. This assignment provides a good way to see all the parts of the pipeline in a single place.

You should construct your cube using the eight vertices (±1, ±1, ±1). You must also draw two coordinate frames (sometimes called gnomons in this context). The first will represent the cube's local modelling coordinates; its origin is the cube's centre, and it will be subjected to every modelling, viewing and projection transformation applied to the cube, except for scaling. The second will represent world coordinates. These will be the same size as the modelling axes, but they will remain fixed at (0,0,0)—they will be subjected only to the viewing and projection transformations. Draw each one so that its x, y, and z axes are visually distinct; the most obvious means of doing so is to draw them with different colours. Though these coordinate frames are conceptually of unit length, you'll probably want to scale them when drawing them in order to ensure they're visible on screen.

You will apply modelling transformations to the cube (rotations, translations, and scales) and viewing transformations to the eyepoint (rotations and translations). The user interface will allow you to select which class of transformation to apply. In each mode, dragging with a combination of mouse buttons pressed will use the x position of the mouse to control the axes on which a transformation will act.

You will need to maintain four distinct coordinate systems in this assignment. Three of these coordinate systems are 3D and one is 2D: the cube ("model") coordinates (3D), the eyepoint ("view") coordinates (3D), the universal ("world") coordinates (3D), and the display ("screen") 2D normalized device coordinates (which arise from the perspective projection of the eye's view onto the eye's xy plane).

The modelling transformations apply with respect to model coordinates (i.e., a model mode rotation about the x axis will rotate the cube about its current x axis, not the world's x axis). The viewing transformations apply with respect to view coordinates (i.e., a view mode rotation about the x axis will appear to swing the objects in view up or down on the screen, since the eye's x axis appears parallel to the screen's horizontal axis). None of the modelling transformations will change world coordinates (i.e., the world gnomon never changes its location, though, of course, it may drift out of our view as a result of viewing transformations).

You are to form all matrices yourself and accumulate all matrix products in software. You will also do the perspective projection yourself, including the division to convert from 3D homogeneous coordinates to 2D Cartesian coordinates. This means that you will have to do a 3D near-plane line/plane clip in the viewing coordinate system to avoid dividing by zero or having line segments "wrap around".

The interface

Your GUI panel must contain at least the following widgets:

The main means of interaction with the environment is by dragging the mouse with one or more buttons held down. When a mouse button is pressed, relative horizontal motion of the cursor is tracked and the transformations are continuously updated until a button up event is received. If multiple mouse buttons are held down simultaneously, all relevant parameters should be updated in parallel. This can be a bit tricky when rotating with multiple mouse buttons simultaneously, since rotations around the different axes don't commute. In this case, you may apply the rotations in a fixed order of your choosing. In general, you will want to be able to compose an arbitrary sequence of transformations.

Here are the interaction modes you must support:

The initial interaction mode should be "Rotate Model", and this mode should be restored on a reset. The amount of translation, rotation, or scaling will be determined from the relative change in the cursor's x value referenced to the value read at the time the mouse button was last moved. Make sure your program doesn’t get confused if more than one button is pressed at the same time; all the motion events should be processed simultaneously, as specified above, although individual “incremental” transformations can be composed in a fixed order/ For example, when rotating around multiple axes simultaneously, you can decide on a fixed order in which the axis rotations will be applied.

You should use appropriate scaling factors to map the relative mouse motion to reasonable changes in the model and viewing transformations. For example, you might map the width of the application window to a rotation of 180 or 360 degrees. On the other hand, do not limit the total accumulation of rotations and translations; i.e., there should be no restriction on the cumulative amount of rotation or translation applied to an object, or to the number of sequential transformations.

Viewport mode

Viewport mode allows the user to change the viewport. Assume that you have a square window into the world, and that this window is mapped to the (possibly non-square) viewport. If the aspect ratio of the viewport doesn’t match the aspect ratio of the window (i.e., the viewport is not square), then the objects appearing in the viewport will be stretched. Further, when you change the viewport, you will see the same objects in the new viewport (possibly scaled and stretched) that you saw in the old viewport. You must draw the outline of the viewport so that we can tell where it is.

In Viewport mode, the left mouse button is used to draw a new viewport. Pressing the left mouse button sets one corner. While the mouse is moving with the button held down, you should dynamically update the viewport, and when the button is released, that viewport should remain in effect. You should be able to draw a viewport by specifying the corners in any order. If the mouse position is outside the window when dragging or releasing the button, clamp the edges of the viewport to the visible part of the window.

The initial viewport should fill 90% of the full window size, with a 5% margin around the top, bottom, left and right edges. This is important so that we can verify that your viewport clipping works correctly—if you do not do this, you may lose marks in two places. The user should be able to set the viewport to any portion of the application window, including sizes larger than the original size. Note also that the viewport is to be reset to the initial size when the reset option is selected from the file menu.

Projection

You must implement a perspective projection. Note that for this assignment there is no need to transform the z-coordinate. Thus you could use the mappings x→x/z and y→y/z directly, although note that some additional scaling will be necessary to account for the field of view. If you do wish to construct a perspective projection matrix, you must do so manually—you may not simply use a library function that creates perspective matrices. That is, you may use a type like mat4 to hold the perspective matrix, but you must construct the matrix with explicit values.

If you cannot get perspective projection working, you may implement an orthographic view (no perspective) instead. You will not get a mark for one of the objectives, but you may still complete most of the other objectives in the assignment. It may actually be useful to implement an orthographic view anyway first in order to get model and view transformations working, and return to add perspective projection last.

Clipping

You will need to clip your lines to the viewing volume. There are several ways to clip, any of which will suffice for this assignment. Note, however, that you must clip to the near plane before performing perspective projection, or you will get odd behaviour and crashes. You may find it easiest to clip to the remaining sides of the viewing volume after projection (since you will be clipping to a cube), but you may clip at any point in your program. Note that we will be testing clipping against all sides of the view volume.

Code

You should already have the necessary starter code in the directory cs488/A2/, which came with the ZIP file you downloaded for A0 and A1. You will make changes to A2.hpp and A2.cpp. This assignment is somewhat unusual, because you will not use any OpenGL API calls directly; instead, you must rely on the provided methods for drawing coloured lines. With that in mind, you should focus on the following additions/changes to the code:

The code you add should contain no OpenGL calls—all drawing is hidden behind drawLine(). In addition, while you are permitted to use most of the vector and matrix manipulation code in the GLM library, do not use the matrix_transform functions, including glm::translate(), glm::rotate(), or glm::scale(). Do not use the function glm::perspective() because that'll defeat the purpose of this assignment. If you use a matrix to implement perspective projection, you must construct that matrix explicitly yourself. You can still use a mat4 to hold it, though. If you're unsure about what functions you are or are not allowed to use, or where you can add code, please ask us.

Deliverables

As always, prepare a ZIP file of the A2/ directory, omitting unnecessary files (executables, build files, etc.). Upload the ZIP file to LEARN. In that directory, include a README file, a screenshot, and a signed copy of a2declare.pdf. If you omit either of the first two files, you will receive a deduction; if you fail to submit the signed declaration, you will receive a 0 on the assignment.

Objective list

Every assignment includes a list of objectives. Your mark in the assignment will be based primarily on the achievement of these objectives, with possible deductions outside the list if necessary.

Assignment 2 objectives