CS 779 - Project

Subdivision Surfaces

by Alex Kalaidjian

Introduction

For my final project in the course CS 779 (Spline Curves and Surfaces), I chose the topic of subdivision surfaces.  Subdivision surfaces basically involves refining some polygonal mesh that forms a surface into another, more smoother, surface with an increased amount of polygons that are smaller in size.  There are several different subdivision schemes out there.  Each one creates a subdivided surface in a different way and the resulting surfaces in turn look different and have different properties.  Subdivision surfaces involves a lot of 3D geometry and math, and requires complicated data structures if you want to implement them on a computer.  I found this topic to be very interesting and enjoyed completing the work pertaining to the project. 

In this webpage, I essentially describe the work that I did for my project.  Firstly, I describe what I did for the base part of my project.  Secondly, I explain the work that I did as extras.  Thirdly, I will illustrate the various subdivision schemes and other features that I implemented with screen shots from my application.  Finally, I will give my opinion on which of the schemes that I implemented are the best, based on my observations from the presented screen shots.

Base Project

For the base part of my project, I implemented three subdivision schemes.  These schemes can be applied to meshes that are made up of polygons that have any number of sides.  In order of increasing complexity, they are:

• Midpoint (sometimes called the simplest scheme)

• Catmull-Clark

• Doo-Sabin

Extras

Additional Subdivision Schemes

The extra work that I completed for my project includes a variety of different things.  Firstly, I implemented three other schemes of varying difficulty.  These schemes can only be applied to meshes containing 3-sided polygons (triangles).  They are:

• Loop

• Root 3

• Butterfly

Note that the Butterfly scheme is interpolating, meaning that the vertices of a subdivided surface are unchanged from the original surface's vertices.

Application

To encapsulate all of the work that I did for my project, I created a full-fledged Windows application.  The features of it include:

• Opening and saving of .s3d polygonal mesh files

• Embedded OpenGL window that allows for model view rotation, panning, and zooming in and out

• Different display modes for the models including:

  • Two kinds of wire-frame modes

  • Lighting based on two different normal calculations

  • Gaussian curvature plots with interactive controls for Gamma and Kmin/Kmax

• Colour selection for the model faces and lines as well as the background

• Ability to apply any subdivision scheme to any intermediate polygonal mesh currently displayed by the application

• Exposes the geometric data of the currently displayed mesh (number of faces, vertices, and edges)

Normals

Although the calculation of the normals for each vertex of a polygonal mesh is not required by the well-known subdivision schemes, implementing it enables lighting calculations that allow a user of the application to get a better feel for the generated subdivided surfaces.  I implemented the calculation of normals for each polygon and for each vertex, both producing distinct and useful visual results.

Data Structures

In order to accommodate all of the different subdivision schemes that I implemented, I created several data structures that store adjacency information between the vertices, edges and polygons of an arbitrary mesh.  In order for them to be efficient as possible, I created them with the heavy use of the C++ STL map class.  They were invaluable while implementing each subdivision scheme.

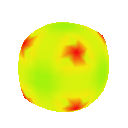
Gaussian Curvature Plot

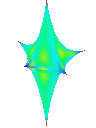
Visualising the curvature of surfaces that have been subdivided can be useful in evaluating the effectiveness schemes used for subdivison.  I implemented an algorithm by Gauss-Bonnet to approximate the Gaussian curvature of a polygonal mesh at each vertex.  I then assign a colour to each vertex based on the calculated curvature value.  This results in a coloured curvature plot across the surface of a polygonal mesh which can easily be used to see the magnitude of curvature at different points on the surface.

Nielson Patch Schemes

I thought of an idea for a new subdivision scheme.  It is to construct a Nielson patch over each polygon of a triangular mesh, and then use this patch to extract new vertices for a subdivided mesh of the original.  A Nielson patch is constructed using three vertices and the corresponding normals at each vertex.  After performing my calculation of normals at each vertex, I have everything I need to construct a Nielson patch over all of the polygons of a triangular mesh.  I implemented two different ways of doing this. 

• One of the ways I implemented is to acquire new vertices for each edge of an original polygon by sampling the patch in the middle of its 3 bounding edges.  These three new edge vertices are combined with the original vertices to refine a triangle polygon into four new triangle polygons, similar to the Loop construction scheme.

• The other way that I implemented a subdivision scheme using a Nielson patch was to sample the patch at its centre to acquire a new face vertex.  New polygons are created here by connecting this new face vertex to other newly calculated adjacent face vertices and to the unchanged vertices of each original polygon.  This is similar to the Root 3 scheme.

Both schemes are interpolating because I use the vertices from the original mesh to create the refined polygons.  For this reason, and maybe others, the Nielson schemes I implemented were not very good.  Perhaps applying some weights to the original vertices to make the schemes non-interpolating would make them better.

Model Creation

Finally, to test out all of the features that I implemented, I created 5 different models that each have different shape properties.  I tested all of my subdivision schemes, normal calculations, and my Gaussian curvature plot construction on each of these models.  The next section includes screen shots that illustrate my results.

Screen Shots

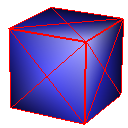
Cube

Midpoint

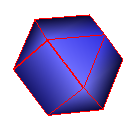
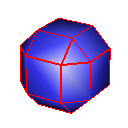
Catmull-Clark

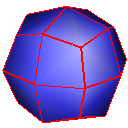
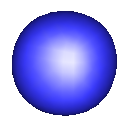
Doo-Sabin

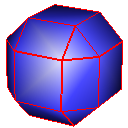
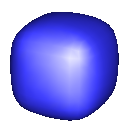
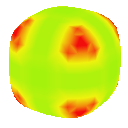
Loop

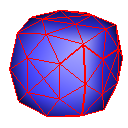
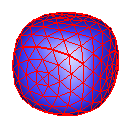
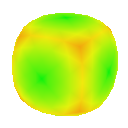
Root 3

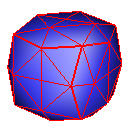
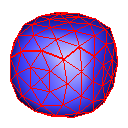
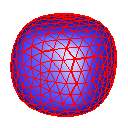
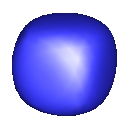
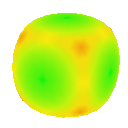
Butterfly

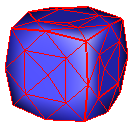
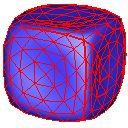
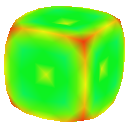
Nielson (New Edge Vertices)

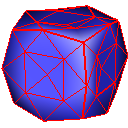
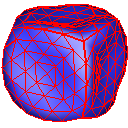
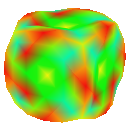
Nielson (New Face Vertices)

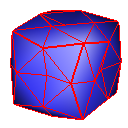
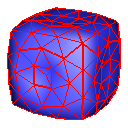
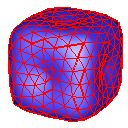
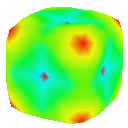
Pyramid

Doo-Sabin

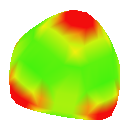
Butterfly

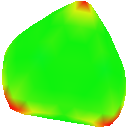
Nielson (New Face Vertices)

Cube with Holes

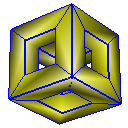
Midpoint

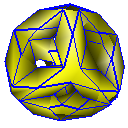
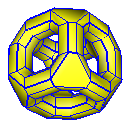
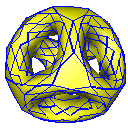
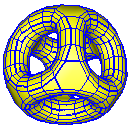
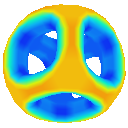
Catmull-Clark

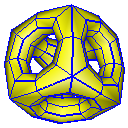
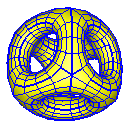
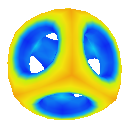
Doo-Sabin

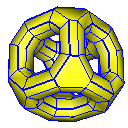
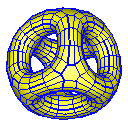
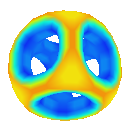
Asymmetric Star

Loop

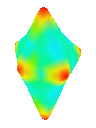
Root 3

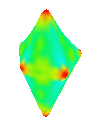
Butterfly

Blob

Catmull-Clark

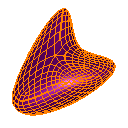
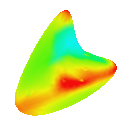
Loop

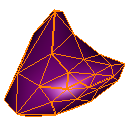
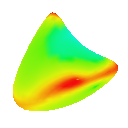
Root 3

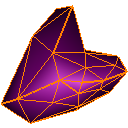
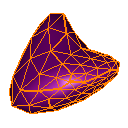
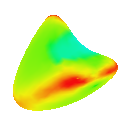
Nielson (New Edge Vertices)

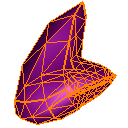
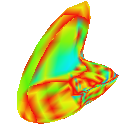
Observations

Based on

• the relative size and shape of each of the subdivided polygons of the subdivided surfaces

• the Gaussian curvature plots of the subdivided surfaces

• the overall subdivision quality and efficiency across all of the characteristically different models

I believe that the Catmull-Clark and Loop subdivision schemes are the best of the 8 that I implemented. 

References

• T. Surazhsky, E. Magid, O. Soldea, G. Elber, and E. Rivlin,

  A comparison of Gaussian and Mean Curvatures Estimation Methods on Triangular Meshes,
  Robotics and Automation. Proceedings. ICRA '03. IEEE International Conference,

  pp. 1021 - 1026 vol.1, 2003

   

• Gerald Farin,

  Curves and Surfaces for CAGD, fifth edition, Academic Press, 2001