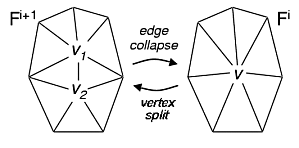
The goal of this project was to implement the construction process of Progressive Meshes, as described by Hugues Hoppe [1]. A Progressive Mesh is a continuous level-of-detail representation of a geometric model, consisting of a low-resolution base mesh M0 and a series of detail records. These detail records are vertex splits, which describe the inverse of the edge collapse operation used to simplify the mesh during the construction phase. Both of these operations are shown below.

A Quadric Error Metric (QEM) can be used to order the edge collapses to yield a good low-resolution approximation of the original mesh [3]. The QEM that I implemented has the following options:
The standard QEM (with the memoryless enhancement turned off) "remembers" information about the original high-resolution mesh, while the memoryless version discards this information as the simplification progresses. While initially counter-intuitive, Hoppe showed that the memoryless version improved the quality of the resulting meshes.
It is also possible to select whether or not vertex normal information should be included in the QEM. If normal information is used, then the QEM incorporates the error in the normal vectors of the simplified mesh as well as the geometric error. Otherwise, only the geometric error is considered.
While this data structure is recommended (in [2]) to efficiently implement progressive meshes once the PM representation has been constructed, it is very awkward to use during the construction process. Other mesh data structures (e.g., half-edge) may be more convenient to use for the construction phase of the algorithm.
 69 451 faces |  9 327 faces |  3 823 faces |
 50 757 faces |  5 455 faces |

After refinement to 745 faces:
| Geometry+Normals | Geometry only | |
| Standard | 
| 
|
| Memoryless | 
| 
|
The memoryless version of the QEM gave much better results for case in which normal error was incorporated into the QEM, although there is a slight improvement in the other case as well. This result is consistent with the results of Hoppe [3].
It is clear that incorporating the normal error into the QEM signficantly degrades the quality of the resulting meshes. I postulate that this is due to the way the normals were generated for the original mesh. Since normal information was not present in the data file, normals were generated for each vertex by averaging the normals of the surrounding faces. The result is a smooth normal field with no discontinuities. However, the geometry of the original model clearly has creases (e.g., along the hairline at the forehead), so this smooth normal field is inaccurate. With normal error incorporated into the QEM, the result is a "smoothing out" of the mesh to match the normal field.