CS679 Project - Loop Subdivision Surfaces Using Triangle Strips and On the Fly Tessalation
I implemented Loop subdivision surfaces. My implementation uses
triangle strips, and has a memory footprint relatively independent of the
subdivision depth. Its architecture is designed to be compatible
with hardware acceleration.
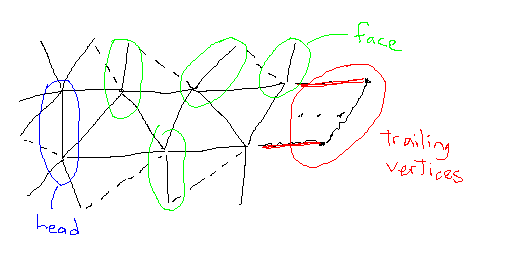
Triangle Strip
The image shows what the basic triangle strip is like. It consists
of a head element containing pointers to the first two vertices and an
array of face elements.
In the regular case of a non-boundary vertex
of degree 6, each face element has a pointer to
the new vertex and a pointer to a neighbour of the new vertex.
To avoid complicated code, all the neighbour pointers except
the ones belonging to the current face's two other vertices
are stored in special cases (<6 vertices, >6 vertices, boundary).
The neighbours of the first and second vertices and the trailing
vertices are also stored in the strip.
Assuming that most of the mesh is regular and the strips are long, we end up
using about 2 pointers per face.
My implementation uses a greedy algorithm for striping a mesh. It starts
with a random face and follows it in a direction determined by
the way the order of the face's three vertices until it
cannot add any more faces to the strip.
Architecture
There are two parts to my program; a software subdivider (A), and a software
module (B) that takes OpenGL-like commands describing a general triangle
strip and tesselates its input to the given subdivision depth.
B is hardware compatible.
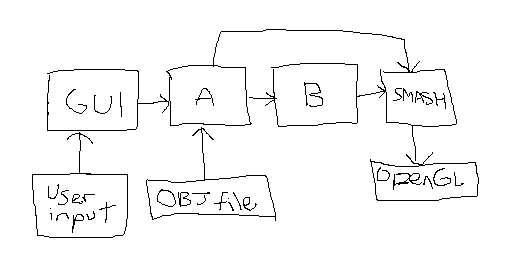
A reads in an OBJ file and converts the mesh into triangle strips.
When told by the GUI to render the mesh, it
passes the regular portions of each strip to B. By "regular portion of
a strip" we mean that the vertices of the faces have degree 6,
and they do not have special tags indicating that non-standard subdivision rules
would be required. Non-regular portions
of strips are subdivided depth-first in A until the required depth is reached
or a regular patch is obtained, whichever is first. If the required depth
is reached first,
the triangle's vertices are projected onto the limit surface and
the projected triangle rendered. Otherwise the regular patch that is
obtained is passed to B to be tesselated.
B is a packet rewriting module that takes a general triangle strip and tesselates
it to the desired subdivision level. It computes the actual
limit surface points of the subdivision surface using forward
differences for the tessalation.
The forward differences
tesselation algorithm is described in Bischoff et. al.
The module has an OpenGL-like API for specifying the triangle strips:
void LoopInit();
void LoopBegin( int m );
void LoopEnd();
void LoopSteer( SurfaceModule::Direction d );
void LoopVertex3fv( point3_t v, int id=0 );
void LoopVertex3f( float x, float y, float z, int id=0 );
void LoopNeighbour3fv( point3_t nb, int id=0 );
void LoopNeighbour3f( float x, float y, float z, int id=0 );
void LoopDepth( uint r );
B uses constant memory; it stores only the last three vertices
(and their neighbours) passed in.
It is hardware compatible.
A stores the mesh data, a full non-compressed (i.e. pointers to all neighbours
of each vertex are stored) representation for the current face being subdivided,
and a full patch representation of the current face at each level of
subdivision. Since subdivision is done depth-first, extra memory usage varies
roughly linearly with subdivision depth. This extra memory is generally small
compared to the memory used by other parts of A.
The subdivision surface to be displayed is generated on the fly;
no data other than the initial strips is stored.
This resulted in a program that was faster at higher subdivision levels
than a comparison program that just output triangles from a prebuilt mesh
on the machine it was tested on because the high memory usage of the
comparison program caused the machine to thrash. At smaller subdivision
levels, the extra cpu time required to reconstruct the neighbour data from the
triangle strips was not noticeable for small meshes, and noticeable for
large ones.
Output for now goes to OpenGL via packet rewriting modules (SMASH in the diagram). The current
GUI is not so great for display.
Note that since the output is a chordal triangle mesh (mesh formed
when you project the control points to the limit surface), as
the number of subdivisions increases the surface may appear to grow
instead of shrink.
What I did Not Write
I did not write the GUI or the SMASH backend, though some modifications were made.
Pictures
Note that the parts subdivided by A and the parts that reached B for
subdividing at depth 0 have vertex normals determined by
averaging the faces around the vertex, and the parts subdivided more than 0
times by B are flat-shaded.
| A general closed mesh with some extraordinary vertices.
Note the shrinkage of the patch handled completely by A, as the other parts
are passed off to B after subdivision by A.
| 
| 
| 
| 
|
| A plane. Demonstrating boundaries and the case where there are only
two neighbours.
| 
| 
| 
| 
|
| A degenerate case. Every vertex has degree 3.
| 
| 
| 
| 
| 
| 
|
Future Work
I didn't have time to implement normals.
Really skinny triangles.
Creases and corners. The framework is there, but there wasn't
time to finish it.
Optimization. Things could go faster.
Acknowledgements
Prof. Mann for giving me the extra time.
Prof. McCool for paper pointers and discussion.
SMASH code (various people). Kevin Moule for the GUI code.
References
K. Muller, S. Havemann. "Subdivision Surface Tesselation on the Fly using a
Versatile Mesh Data Structure".
Eric Halls' thesis.
H. Biermann, A. Levin, D. Zorin. "Piecewise Smooth Subdivision Surfaces with Normal Control".
S. Bischoff, L.P. Kobbelt, H. Seidel. "Towards Hardware Implementation of Loop Subdivision".























