CS 679 - Subdivision Surfaces , 1999

Vincent Ma

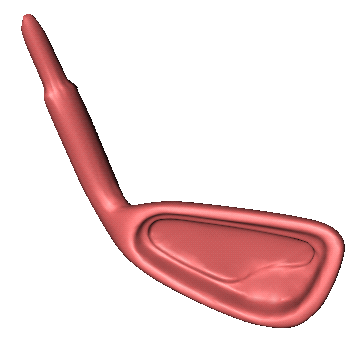
The goal of this project is to give a visual comparison between different subdivision schemes. Given a certain control mesh to start with, I wanted to show the kind of surface each scheme produces.

There are 3 schemes implemented in this project:

Simplest Subdivision Scheme (or Peters as I'd like to call it) which simply takes the midpoints of each edge and connects to other midpoints of those edges that are adjacent and share a face. Then, new faces are created, one for each old face, and one for each old vertex. This scheme generalizes the "4-direction box-spline".
Catmull-Clark
With this scheme, new vertices are calculated for each face, edge and vertex of the original mesh, then, for each vertex, a new face is created that spans the new vertex, "midpoints" of pairs of old edges, and the face vertex. This scheme generalizes bicubic B-spline surfaces.
Doo-Saban
For each vertex-face pair, a new vertex is created. Then, connecting these in an appropriate way will create a new face for each old face, edge, and vertex. This scheme generalizes biquadratic B-spline surfaces.

To implement these I first implemented a Half-Edge data structure that will store the polygonal data. The half-edge structure will allow me quick access between adjacent vertices/edges/faces and it theoretically will speed things up.

On top of this data structure I added functions to evaluate the face, edge and vertex points that I needed for evaluating each different subdivision scheme.

Finally, I added a GUI that allows a user to interactively view a control mesh and the resulting subdivision surface.

In addition, I've implemented "infinitely sharp edges" for the Catmull-Clark subdivision scheme. Essentially, it means that for edges that are labelled "sharp" different rules will be used to calculate the edge/vertex points used in the subdivision calculation.

In the GUI, the user can select one or more edge. Selected edges are tagged as sharp. By selecting different sets of edges, the user can create differently shaped surfaces from a single common control mesh.

The user can save the result surface out to Inventor format files viewable in "ivview".

References

T. DeRose, M Kass, T Truong, SUBDIVISION SURFACES IN CHARACTER ANIMATION Computer Graphics. Pages 82-94, 1998
E. Catmull, J. Clark. RECURSIVELY GENERATED B-SPLINE SURFACES ON ARBITRARY TOPOLOGICAL MESHES. Computer Aided Design, 10(6):350-355, 1978
G. CHAIKIN. AN ALGORITHM FOR HIGH SPEED CURVE GENERATION. Computer Graphics and Image Processing, 3:346-349, 1974
M. Halstead, M Kass, T DeRose, EFFICIENT FAIR INTERPOLATION USING CATMULL-CLARK SURFACES. Computer Graphics 27(3):35-44, Aug 1993
H. Hoppe et al, PIECEWISE SMOOTH SURFACE RECONSTRUCTION. Computer Graphics, 28(3):295-302, July 1994
J Peters, U Reif, THE SIMPLEST SUBDIVISION SCHEME FOR SMOOTHING POLYHEDRA. March 4th, 1997
A. Holden, SHAPES, SPACE, AND SYMMETRY. Columbia University Press, 1971
K. Joy, ON-LINE GEOMETRIC MODELING NOTES, http://graphics.cs.ucdavis.edu/CAGDNotes/ November 7, 1996