M02: Functions

This lecture module is the start of the actual course content. It has more video content than will be typical because there is some stuff that’s easier to just show, some that benefits from body language, and some that is simply important to reinforce for multiple learning styles.

Boxes:

• The green “exercise box” signals something to do. Take a moment to solve the problem. We think it will help you understand the course content more thoroughly. In this case, working out how many natural numbers divide 12 evenly will help you understand the next point.
• The box with an ! on the left is a “don’t box”. It is used in a couple of circumstances:
  • To pose a question we want you to think about but not solve (like this case).
  • To highlight something you should not do, for example on assignments.

Finding the number of divisors of 12 is reasonable to do by hand. But doing the same thing for 5,218,303 is too difficult to solve by hand in a reasonable amount of time. Our task in this course will be to write instructions to allow the computer to solve tasks such as these.

Instead of solving this particular problem, we will write a function that solves the problem in general, for any number.

We can test our function using small numbers like 12, 31, and 63. Once we are confident the function is correct, we can use it to answer the “big” question.

This video discusses programming language design and why we’ve chosen a functional programming language (Racket) rather than a more traditional choice. We then review some of the core concepts that functional programming languages borrow from mathematics.

Video: Download m02.01_pl_design

There are three fundamental problems that programming language designers must solve for their programming language:

• How programs are expressed (the syntax)
• What programs mean (the semantics)
• Ensure that each valid program has exactly one meaning (avoid ambiguity)

Syntax has to do with the form or structure of something. The sample sentence does not have the expected structure – first word begins with a capital letter, punctuation at the end, etc.

“Trombones fly hungrily.” is a syntactically correct sentence. It has the expected form/structure. But semantically it is meaningless. Trombones don’t fly nor do they get hungry. Note that we are referring in this example to the real world rather than a constructed world in a fantasy novel or poetry where there might be flying hungry trombones.

That said, the semantics of our programs will be with respect to the constructed world of our programming language.

English can be ambiguous. In “Sally was given a book by Joyce” it’s unclear whether the person giving the book was named Joyce or the person who wrote the book was named Joyce.

Another example is “Time flies like an arrow”. One possible meaning is that time passes quickly. But another meaning parallels the sentence “Fruit flies like a banana.” There are several other possible meanings as well.

It’s very helpful to be able to predict what your program means (what it will do) while you are writing it. If you can’t, you’re no better than one of those proverbial monkeys banging on a typewriter trying to come up with Shakespeare.

Fortunately, Racket allows us to develop a simple semantic model that we can use to predict what a program does.

There are other reasons we chose Racket for CS135. Watch the video for more about that.

The following video introduces the DrRacket programming environment and the core features to get you started programming.

Video: Download m02.10_dr_racket

You will be changing language levels periodically as you become a more experienced programmer. Changing these settings, in this manner, will be required each time.

Rational numbers are those that can be represented as a ratio between two integers. For example, 22/7. Irrational (“inexact”) numbers cannot be written as a fraction. Examples include π and the square root of 2.

A calculator doesn’t make much distinction between the rational and irrational numbers. A calculator displays π as 3.141592654 and 22/7 as 3.142857143. There is nothing to distinguish the rational number from the irrational number.

Racket does make the distinction. Use rational (“exact”) numbers whenever you can.

The n^th argument is associated with the function’s n^th parameter. For example, in g(1,3), the first argument (1) is associated with the first parameter (x). Each place that x is used, substitute 1. Similarly, each place y is used, substitute 3.

“Evaluation by substitution” means to take a subexpression, find its value, and then replace the subexpression by the value (that’s the “substitution” part). Repeat until you’re left with just values.

If you choose a complicated subexpression you may need to use “evaluation by substitution” to find its value.

This notion of evaluation by substitution is an important one. We’ll be defining rules to make this rigorous and then adding to those rules as we introduce new language constructs. You’ll get the first taste of them in just a few slides.

Noting the two conventions as the end of the slide, consider g(g(1,3), f(3)) again. We can’t apply g to g(1,3) and f(3) because of the first rule – g(1,3) and f(3) are not values.

So we have a choice to make. Should we evaluate the subexpression g(1,3) or f(3) first? The second rule says to do the leftmost one or g(1,3).

Stated another way: read the expression from left to right, top to bottom.
Substitute the first function application that has fully evaluated arguments.

Review the derivation on the previous slide. Verify that these two conventions were obeyed at each step.

Now, for any expression:

• there is at most one choice of substitution;
• the computed final result is the same as for other choices.

This video is the transition from mathematical notation to Racket notation. The slides give a good overview of the changes. The video can help solidify your understanding of how to transform the traditional mathematical notation to Racket notation.

Video: Download m02.31_notation

To transform from traditional mathematical notation to Racket notation, proceed as if you were evaluating the expression via substitution. But instead of substituting back the value, substitute the expression re-written as Racket.

For example:

(6 - 4) / (5 + 7) ⇒
(- 6 4) / (5 + 7) ⇒
(- 6 4) / (+ 5 7) ⇒
(/ (- 6 4) (+ 5 7))

Note that the first line is valid math; the last line is valid Racket; the middle lines are a mixture.

You can test your understanding by transforming mathematical expressions to equivalent Racket expressions. Then enter them into DrRacket to verify that they give the correct answer.

An example of “extra” parentheses in math: (2 + 3). The parentheses add nothing to simply writing 2 + 3. If you translate this literally you would get the Racket expression ((+ 2 3)). The outside set of parentheses will cause Racket to “think” it needs to apply a function, but there is no function specified to apply.

We also have a tool to show the substitution process interactively. Play around with the following to see how it corresponds to what is on the slide and how it implements the rules we’ve seen so far.

Here’s our first substitution rule.

Essentially, the rule says that we just “know” what the built-in functions do. It might be because we’ve studied them since early grade school (+, *, etc) or because we’ve read the DrRacket documentation (string<?). Use this knowledge to compute the result for the given arguments (which will be values) and then substitute that result into the expression in place of the function application.

In the stepper, this rule has the name “as-if-by-magic” because we don’t try to explain how the built-in function works.

It’s a great idea to fire up DrRacket and enter these into the interactions window. Learning what the various error messages mean on these small examples will help you debug your assignment problems more efficiently.

The third one is “interesting”. Watch the video to understand what’s going on.

Video: Download m02.32_errors

Here’s a video showing how to find the list of built-in numerical functions available in our language level.

Video: Download m02.33_documentation

Here’s a direct link to the Help Desk documentation .
Bookmark it! For technical documentation that’s a better strategy than Googling it every time. There is less risk of getting out-of-date material.

Defining functions is the core activity in programming in Racket. This video covers the syntax, reviews applications of functions to arguments, defining constants, etc.

Video: Download m02.40_def_functions

Special forms are typeset just a little differently in the slides. A special form, like define is in a bolder and slightly darker font than a normal function. If you skip ahead to M04 you’ll notice that and, or, and cond are typeset the same way. They’re also special forms. Unfortunately, we’re not completely consistent. else is also typeset this way but is not a special form.

Verify that the two rules given are used to choose the next subexpression to evaluate.

A Racket program is read top-to-bottom, left-to-right. That is,

(define (foo x y) (+ x x y))
(foo 1 2)

is read as

(define (foo x y) (+ x x y))  (foo 1 2)

The function definition is already as simple as it gets, so (foo 1 2) is the left-most subexpression that we can simplify. Furthermore, (define (foo ... occurs to its left, as required by the substitution rule.

Evaluating (foo 1 2) means substituting the first argument (1) wherever the first parameter (x) occurs in the body expression and doing similarly for the second argument/parameter. That gives us (+ 1 1 2). That expression is substituted back in place of (foo 1 2).

That is,

(define (foo x y) (+ x x y))  (foo 1 2)
⇒ (define (foo x y) (+ x x y))  (+ 1 1 2)

Recall that => means “yields” and separates one substitution step from another.

Or, with the stepper. You’ll notice in the “Rule” section that it calls this rule “Big-sub”. We’ll have another rule named “Small-sub” soon.

Rules so far:

1. (f v1...vn) => v when f is built-in…
2. (f v1...vn) => exp' when (define (f x1..xn) exp) occurs to the left…

An in-depth explanation of the trace shown in the slide:

The fact that parameter names are local to the function is really handy. It means that you can choose their names without regard for the rest of the program. You can focus on deciding which names make sense for the function, given its purpose.

The parameter names as used in the slides so far won’t be acceptable once we move beyond toy examples to functions that do something meaningful. Then we’ll want parameter names that convey meaning about their purpose in the function.

We can see this example in action in the following stepper. Note that completely processed definitions that will not change are at the top of the listing followed by a blank line. k is already completely defined and starts out above that blank line.

p will move up after it’s completely defined in the fourth step. foo is also completely defined but doesn’t get to move up until the definitions preceding it are completely defined.

Function definitions are always in simplest form and aren’t further reduced. That’s not necessarily the case with constant definitions. Notice that the right hand side of id => val is a value. If the expression starts as (define p (* 3 3)) the (* 3 3) must be simplified to 9 first.

This is illustrated in the stepper with the next slide. Note that the stepper gives this rule the name “small-sub”. For both a constant and a user-defined function we’re making a substitution. For the constant, it’s a pretty small substitution; for a function, it’s always much bigger.

The convention that we stop repeating a definition is represented in the stepper by moving the definition above the blank line. Without this convention we would need to copy the entire program for every step. This convention will benefit you big time when it comes to writing exams!

Comments are for the benefit of humans. The computer ignores them.

Repeating code leads to several problems:

• If there is a bug in the repeated code, it needs to be fixed multiple times. Some places may be missed.
• The programmer has to spend time typing the same thing multiple times.
• The repeated code may be useful elsewhere but can’t be easily reused.
• The repeated code is difficult to test. In a rigourous testing environment, it may force many additional tests that are essentially the same.
• Someone reading the code needs to stop and figure out what the code does, interupting the flow of understanding the main function.

Using constants and helper functions are both examples of the “DRY principle” – “Don’t Repeat Yourself”.

Being DRY reduces the amount of code you need to write, debug, and maintain. If there is a bug, there’s only one place to go to fix it.

Factoring out complex calculations gives a separate function that is usually easier to test.

Humans can’t keep too much in our heads at once. We need to chunk things. Factoring out calculations into a helper function is one way to do that. It’s often worth it even if the helper function is only used once.

Having meaningful names in the code to identify an operation also helps with that chunking. “Oh yeah, I know what that does.”

Programmers can use the interactions pane to do one-time testing, or they write their tests using check-expect. Using check-expect is preferrable because:

• All you need to do is click run to re-run all of the tests you’ve developed.
• The interpretation of the test (did it pass or fail?) is built in to the test. That isn’t true if you just say (distance 0 0 3 4).
• It’s less error-prone. Even tests sometimes need to be debugged!

You are welcome to use check-expect on Assignment 01 but it is not required. Starting with A02, testing with check-expect will be checked and will be expected.

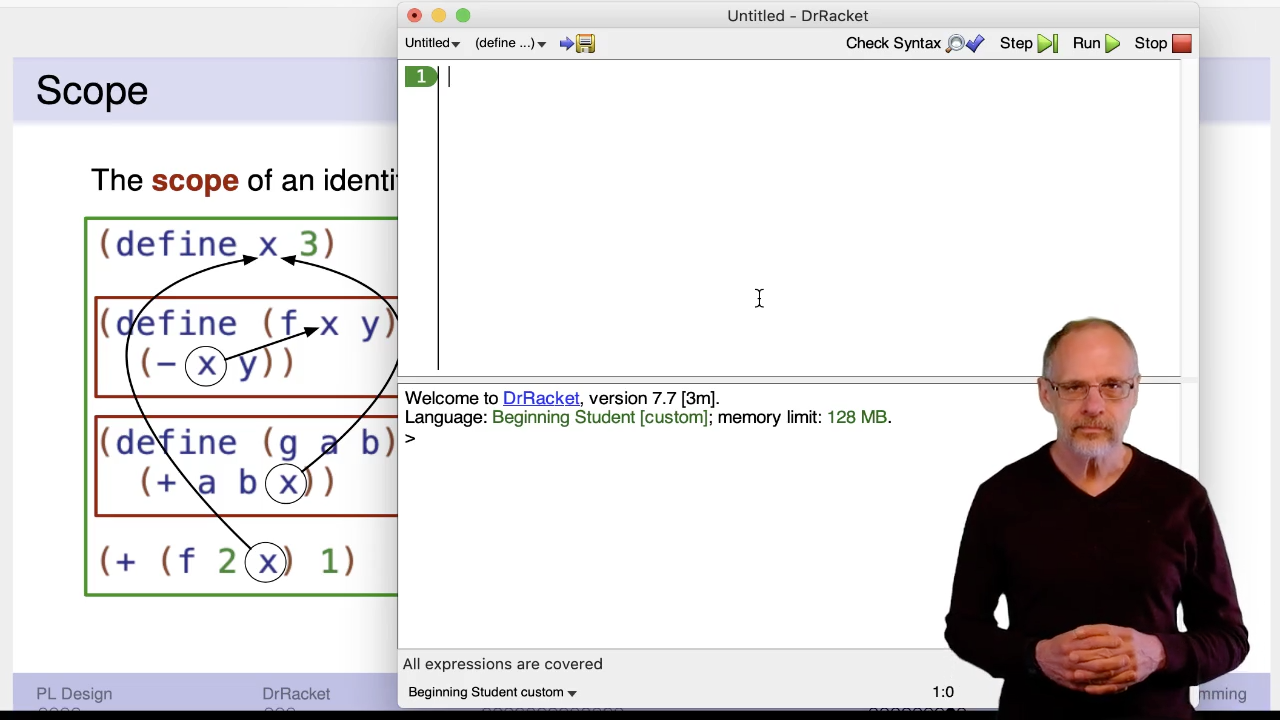
The next video shows how DrRacket can help you determine the scope of an identifier.

The x parameter in function f is said to “shadow” the global constant x.
Another way to say it is that x “hides” the global constant.

This video is almost entirely in DrRacket to show you the definitions window and how to use it to define functions. There are a number of tools built into DrRacket that are covered:

• a stepping tool that may be helpful for debugging your functions
• a tool to help you with scoping issues
• a feature that helps you identify code that hasn’t been tested (making sure everything is tested is a core skill for earning a high mark in CS135!)
• a feature that automatically formats/indents your code for you.

Video: Download m02.50_programming