M06: Lists

You probably already have an intuitive idea of what a list is. Go with that intuition.

A list is a value. That means it’s as simple as it gets; no further simplification can be done.

This notation for a list, with all the cons in it, is admittedly ugly and a pain to work with. We use it to introduce lists because it reveals their underlying structure. That’s important for understanding how to work with lists.

Once we understand lists thoroughly, we’ll construct lists using a much simpler notation.

This slide also shows a way of visualizing lists. The empty list is shown as a solid black bar. You’ll see it at the end of every list. Elements of a list are shown as boxes.

Lists are typically drawn with empty on the right. The first item to be added will be right beside it. The most recently added item will be on the left. This also matches the order in which the Racket code is written.

If you have programmed before, this may look a lot like an array. It’s not. The computer can easily access the i^th element of an array. That’s not the case with a list. Lists are more restrictive but have other advantages.

In general, a list of n items is an item followed by a list of n-1 items – with the caveat that a 0-item list is special.

Lists can be built up, one item at a time, with cons. The simplest list is the empty list, signified by the value empty. Every list we build adds additional items to an empty list.

The primary tools for extracting values from a list are first and rest. They may be used in combination to extract any value in the list.

The following will extract the second item, "eggs", from the list.

The list of primitive (most basic) functions on lists is short and sweet. Watch the video to learn more.

Video: Download m06.30_basic_constructs

Each v and lst on the slide could have been produced by an expression. For example, (cons (+ 1 2) empty) is valid because (+ 1 2) evaluates to a value and empty is a list value.

This function will not work if the list has only one number or is empty. That’s reflected in the contract’s Requires clause.

There’s new notation, (listof Num), for the contract. We’ll explain more soon.

If a function produces a Boolean value it may be more natural to write the body as a Boolean expression. A first attempt seems simple: check if the first element of the list (that is, (first loc)) is the same as the second element, (first (rest loc))).

That works great, as long as the list is at least two elements long. If there are either zero or one wishes it fails miserably when either first or rest is applied to an empty list (try it!).

The function makes use of short-circuit evaluation to avoid those errors. The order of the arguments to and matters. The check for whether loc is empty must come first (why?).

Four examples are illustrated on the right side of the slide.

The functions on the previous slides include contracts but using a new notation. Let’s understand that notation. The fundamental question is “list of what?”.

The left-hand-side of the contract should be as general as possible. If your function can correctly process a list of numbers such as (cons 1.1 (cons 22/7 empty)) use (listof Num) in the contract rather than the overly restrictive (listof Int) or (listof Nat).

On the other hand, the right-hand-side of the contract should be as specific as possible. For example, if your function always produces a natural number, use Nat in the contract rather than Int or Num.

We don’t currently have a way of writing a contract for a function consuming a list of strings and symbols such as (cons "Hello" (cons 'world empty)) – but we will.

Reviewing the contracts for add-replace and first-two-equal? indicates they both consume a list of wishes. wishes are represented by strings, so they both consume a (listof Str). add-replace produces a string; first-two-equal? produces a Boolean. So their contracts are:

add-replace: (listof Str) -> Str
first-two-equal?: (listof Str) -> Bool

Formalizing list values (the top three lines of the slide) show us how to construct new list values.

• empty is a value, by definition.
• (cons 1 empty) is a value by the second rule and the fact that 1 and empty are both values.
• (cons 2 (cons 1 empty)) is a value by the second rule and the fact that 2 is a value and, as we just established, (cons 1 empty) is a value.
• (cons "code" (cons 2 (cons 1 empty))) is a value by the second rule and the fact that ….

We can also run that logic backwards. “(cons 1 (cons 2 empty)) is a list by the second rule and because 1 is a value and (cons 2 empty) is a value. We know that (cons 2 empty) is a value by rule 2 because 2 is a value and empty is a value.”

We now add substitution rules for lists to our existing list of fourteen substitution rules, with examples of two in action.

There’s no substitution rule for cons because of its role in list values. If we would include it, it would be

(cons a b) => (cons a b) where a is a value and b is a list.

In other words, “an X is an X”. And how do we know not apply the substitution rule again? And again. And again. So, it’s not included.

Understanding the next dozen slides is really important. Data definitions, templates, and recursion are core concepts in CS135. Watch the videos in addition to reading the slides and doing the exercises.

Video: Download m06.40_data_def

We can use this data definition to show rigorously that (cons "a" (cons "b" empty)) is a (listof Str):

According to the data definition, it is a (listof Str) if (and only if) "a" is a string and (cons "b" empty) is a (listof Str).

"a" is certainly a string.

Is (cons "b" empty) a (listof Str)? (Hint: Yes. Thank about why.)

Because the template will be used many times to create functions, the video goes farther than the slides and includes as much of the design recipe as possible (nothing in the design recipe goes away once we start using templates). The video also suggests a way to integrate the template with your function development workflow.

Video: Download m06.50_template

Here’s the template developed in the video, except that it had a few extra ...s.

;; (listof-X-template lox) PURPOSE
;; Examples:
(check-expect (listof-X-template empty) ANSWER)
(check-expect (listof-X-template (cons X empty)) ANSWER)

;; listof-X-template: (listof X) -> Any
(define (listof-X-template lox)
  (cond [(empty? lox) ...]
        [(cons? lox) (... (first lox)
                          (listof-X-template (rest lox)))]))

(Note: We changed the example for lecture since this video was recorded. It’s essentially the same function.)

Video: Download m06.60_count_concerts

Craig S. Kaplan created a wonderful video for CS115, The Parable of the Clones, to illustrate summing the elements of a list of numbers. It is absolutely worth 5 minutes of your day to watch it.

Video: Download m06.65_clones

These four questions are going to come back over and over.

In the case of count-wishes:

1. The length of an empty list (the base case) is 0.
2. (count-wishes (rest loc)) should produce the length of the rest of the list, an integer.
3. We don’t care what the first value is, just that it exists. There’s no need to transform it.
4. We should combine steps 2 and 3 by adding 1 (because the first element exists) to the result of step 2.

Note that the only parts of the solution that are not in the template are the 0 and the + 1.

Unfortunately, we’ll be seeing less of our stepping tool from now on because it doesn’t support condensed traces.

Examples of “a smaller version of the same problem” that we will encounter later in the course:

• A list that is one element shorter (terminating at the empty list).
• A number that is one smaller (terminating at 0).
• A set that has fewer elements (terminating at the empty set).

Fire up DrRacket and write this code! Be sure to make use of the listof-X-template.

A lot of the design recipe has already been done for you. Study it before going on to actually write the function body.

Think about the “four crucial questions” from earlier in the module:

1. What should the function produce in the base case?
2. What should the function do to the first element in a non-empty list?
3. What should applying the function to the rest of the list produce?
4. How should the function combine #2 and #3 to produce the answer for the entire list?

As you answer each of these questions, fill in the corresponding part of the template.

Copy and paste your code for count-bicycles and adapt it to count-string. Or go through the whole design recipe from scratch – it would be good practise!

This is the final form of the listof-X-template. You may (should!) use it in your assignments for functions that consume a list. You do not need to include it explicitly.

Many people replace (cons? lox) with else. The advantage is brevity; the disadvantage is a bit less help from DrRacket if you accidentally apply the function to something that isn’t a list.

On assignments we may ask you to make templates for other data definitions.

Simple recursion is easier to use than other forms of recursion (accumulative, mutual and generative). We are introducing patterns of recursion as guidance for you so that you can steer clear of the other (harder) forms until we have need of them.

This is a rule of thumb or heuristic for identifying simple recursion. It is based entirely on the recursive application – on that specific place or places in the code where the function applies itself again.

In the first example, the only argument is one step closer to the base case (lst with the first element removed). Note that the data definition is in terms of the first element and the rest of the list. So “one step closer to the base case” means removing the first element. A list that is one item shorter is not “one step closer to the base case” unless it is shorter because it’s missing the first element. Removing the second element doesn’t count!

The second example is like the first except that there is an additional parameter that is passed along unchanged. The count-string exercise is an example of this.

In the third example, process is meant to capture doing something to lst other than removing the first element. In the fourth example, math-function applied to x indicates that x is changed. In both cases, the function is no longer “simple recursion”.

DrRacket’s Help Desk contains documentation for all of the built-in list functions. There are a lot of them that CS135 students will never need or use. Trust us that we’ll tell you about the ones that are useful when the appropriate time comes.

In the mean time, a few notes:

1. In addition to the ones we’ve already covered (cons, first, rest, empty?, cons?, list?), the useful ones are append, length, member?, remove, and reverse. But don’t use append, member?, remove, and reverse until we introduce them.
2. Functions that begin with ‘c’, end with ‘r’ and have a mixture of ‘a’s and ’d’s in between are historical relics from Lisp. An example is caddr.
   The updated versions in Racket are first, second, third, etc. first is used A LOT. second … eighth are used only very occasionally. However, at this point in the course you are only allowed to use first.
3. We will often state that you cannot use a particular function in a given problem or assignment. You’ll lose marks if you violate that. Why do we do it? To guide you to a particular insight or solution that we think is important.

In the past, some students have written code using (= (length lst) 0) instead of the equivalent (empty? lst). To see why this is a bad idea, use the following steppers to answer these questions:

1. Approximately how many times must you click “Step Forward” to reach the final answer of (= (length abc) 0)? Approximately how many times must you click “Step Forward” to reach the final answer of (empty? abc)?

   • 36-38, 5-7
   • 39-41, 5-7
   • 42-44, 5-7
   • 45-47, 5-7
   • 48-50, 5-7

2. Does (= (length lst) 0) always produce the same result as (empty? lst)?

   • Yes
   • Yes, provided lst is a list
   • No

So far all our list functions have produced a single value – a number or a boolean. But there’s no reason it can’t produce a list. The contract specifies that negate-list produces a list of numbers.

The function so far is simply the listof-X-template with the function renamed to negate-list.

Consider the four questions from earlier:

1. What should the function produce in the base case?
   This is answered by the first example. It’s a great idea to include the base case(s) as example.
2. What should applying the function to the rest of the list produce?
   A list of those numbers, negated.
3. What should the function do to the first element in a non-empty list?
   In this case, negate it. We already have (first lon) to get the first element. All we need to do is add (- ...) around it.
4. How should the function combine #2 and #3 to produce the answer for the entire list?
   In count-wishes we combined 1 and the recursive application (another number) using +. In sum you would also have combined the first number with the recursive application (another number) using +.
   
   Here, we’re combining a number with a list (the result of the recursive application). + doesn’t work.
   So what operator do we have to combine a value with a list? cons.

This produces a full trace; not the condensed trace shown in the slide.

Try to come up with the non-empty list data definition and template on your own. Then watch the video.

Video: Download m06.70_nelist

In the (listof X) data definition, (listof X) is the name.

That name is not used in the first clause – empty – which is the base case.

That name is used in the second clause, which shows how to build a “larger” version of the data (a list with one more element).

Recall that Racket (and most other languages) represent a string value with double quotes: “Hello, world!” or “To be, or not to be, that is the question.”

Racket has quite a few string-processing functions built-in. Examples include string-append, string-downcase, string-length, and substring (See the Help Desk for more details.)

But what if those functions didn’t exist or we needed something very specific for our project? We need a way to rip a string apart into its underlying characters, work on those characters, and then (maybe) put them back together again.

Check it out in DrRacket’s interactions pane! Type in (string->list "Funky @*π012é") to see what you get. Use cut-n-paste if you don’t know how to produce π on your keyboard.

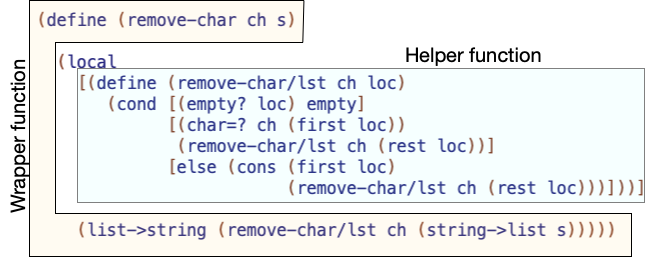
Note the contract. This is the first function we’re writing that consumes a character (abbreviated Char) or a (listof X) where X happens to be a character.

The characters in the list don’t seem to have any specific meaning, so naming the parameter based on its structure is OK. loc is short for “list of characters”.

In some of the tests the author chose to spell out the list of characters explicitly. In the last the author chose to use string->list to easily generate the list of characters from a string. Either approach is fine.

To solve the problem, consider the “four crucial questions” from earlier in the module:

1. What should the function produce in the base case?
   The base case is an empty list. There is nothing to remove; produce an empty list.
2. What should applying the function to the rest of the list produce?
   The rest of the list of characters – without the specified character
3. What should the function do to the first element in a non-empty list?
   We need to compare the first character in the non-empty list with the ch. If it’s the same, we skip over it (remove it); if it’s different we need to keep it.
4. How should the function combine #2 and #3 to produce the answer for the entire list?
   Depending on the chararacter, cons them together or not.

The term wrapper function will make more sense when we introduce the local special form in a few weeks. Then we will be able to literally wrap the wrapper function around its helper function.

“Non-decreasing order” can accomodate duplicates. If we simply said “increasing order” we couldn’t. That is, (sort (list 2 2 3 2 1)) is fine and produces (list 1 2 2 2 3).

To solve this problem, we have two complimentary approaches: using the templates and considering our four crucial questions from M06:

1. What should the function produce in the base case?
   The base case is an empty list. A sorted empty list is still just the empty list.
2. What should calling the function on the rest of the list produce?
   It should produce the rest of the list in sorted order.
3. What should the function do to the first element in a non-empty list?
   Probably nothing. sorting a list shouldn’t change the individual elements, just rearrange them.
4. How should the function combine #2 and #3 to produce the answer for the entire list?
   The first element needs to be put at the correct location in the result of the recursive application (a sorted list) so that the entire list is sorted.

Here’s the code for insertion sort, ready to pop into DrRacket.

;; (sort lon) sorts the elements of lon in non-decreasing order
;; Examples:
(check-expect (sort (cons 3 (cons 4 (cons 2 (cons 5 (cons 1 empty))))))
              (cons 1 (cons 2 (cons 3 (cons 4 (cons 5 empty))))))

;; sort: (listof Num) -> (listof Num)
(define (sort lon)
  (cond [(empty? lon) empty]
        [else (insert (first lon) (sort (rest lon)))]))

;; (insert n slon) inserts the number n into the sorted list slon
;;     so that the resulting list is also sorted.
;; Example:
(check-expect (insert 3 (cons 1 (cons 4 (cons 5 empty))))
              (cons 1 (cons 3 (cons 4 (cons 5 empty)))))

;; insert: Num (listof Num) -> (listof Num)
;;   Requires: slon is sorted in non-decreasing order
(define (insert n slon)
  (cond [(empty? slon) (cons n empty)]
        [(<= n (first slon)) (cons n slon)]
        [else (cons (first slon) (insert n (rest slon)))]))

We’ll come back to sorting in M17 when we study Quicksort. The end of this module discusses merging two sorted lists , which represents a large fraction of the Mergesort algorithm.

DrRacket can provide a trace automatically. This can be a substantial help in debugging your programs!

To use this, you’ll need to do some one-time set-up. This may have been required as part of A00; if so, you don’t need to repeat it. Otherwise, go to Assignments -> Racket and DrRacket and install uwaterloo-racket-tools.

You need to make a couple of changes to your program to enable tracing:

• Add (require htdp-trace) at the top of your program.
• Substitute define/trace for define in each function you want to trace. This implies that you don’t need to trace everything – only those functions that you need to debug or understand better.

The trace tells you three important things:

1. The arguments for each traced function application (e.g. sort is being called with the list (cons 3 (cons 2 (cons 5 (cons 4 empty))))). Note the compact representation of a list. Function applications are represented with one or more > signs.
2. What the applied function produces (e.g. (), which represents the empty list). One or more < symbols indicates that a function has terminated and is producing a value.
3. The depth of recursion. The > > > preceding (sort ()) indicates that application is nested three levels deep.

“additions made to the semantic model” means the new stepper rules.