M14: Functions as Values

What are the values we’ve discussed so far? Numbers like 3 and 1/4, symbols like 'earth, strings like "Hello, world!", and Booleans like true or false.

More complex values include lists like (cons 1 (cons 2 empty)) and structures like (make-point 3 4).

In Racket, functions are also values! That means you can do the same kinds of things with functions that you can do with other values like 3, "Hello, world!", and (list 1 2 3). Functions can consume them and produce them, they can be bound to identifiers and contained in lists and structures.

For example, we have written lots of functions that consume a list as an argument. Now, we’ll start writing functions that consume a function as an argument. This sounds weird, but is very useful!

Notice how + and append are substituted into the body of foo wherever f occurs – just like 2 and (list 'a 'b 'c) are substituted everywhere x occurs within foo.

In a text editor or DrRacket, do a search-and-replace:

• replace keep-odds with my-filter
• replace eat-apples with my-filter

Both functions will now be the same except for the predicate, (odd (first lst)) in one and (not (symbol=? (first lst) 'apple) in the other. Note that both are operating on the first element in the list.

That single difference can be passed as parameter to the function, as we see in my-filter.

This is a condensed trace; it only shows the most important parts.

The first thing to note is that in the first substitution step, even? is substituted into the body every place pred? occurs – just like (list 0 1 2 3 4) is substituted in every place lst occurs.

The result is a very normal-looking cond expression. Evaluate it (skipping several steps) to arrive at the next step shown.

The traces for (filter even? (list 0 1 2 3 4)) and (my-filter even? (list 0 1 2 3 4)) are very different because one is built-in and the other isn’t.

Here’s the complete trace using filter:

(filter even? (list 0 1 2 3 4)) ⇒ 
(list 0 2 4)

Functions like eat-apples that require a custom predicate are often ideal candidates for local. For example, instead of the code shown on the slide, consider

(define (eat-apples lst)
  (local [(define (not-symbol-apple? item) 
             (not (symbol=? item 'apple)))]
    (filter not-symbol-apple? lst)))

Yes, it’s slightly more code. But remember all the software engineering benefits of using local.

In M16 we’ll see a more compact way of writing this.

1. Code size:
   (define (keep-odds lst) (filter odd? lst)) is certainly more compact than the original version of keep-odds.
2. Cut-and-paste: If a program already contains keep-odds and now needs keep-evens, a programmer will likely cut and paste the keep-odds function and then modify it. On the one hand, that’s good because it can save time and leverages work that’s already been done. On the other hand, it violates the DRY principle . Code is replicated; both sets of code must be maintained; bugs may be replicated and (more likely) needed changes missed. Abstracting out the common code addresses all these issues.
3. Bugs: filter is pretty simple and hopefully doesn’t have any bugs. But if it did, fixing filter will fix that same bug across all the places where it is used. This isn’t limited to higher order functions. It applies to any time you’re being DRY and moving common code to a function.
4. Other beneficial changes, besides fixing bugs, may be to increase the speed or increase the size of problem that can be handled by the function. Once again, doing it once spreads these benefits to each place the function is used.

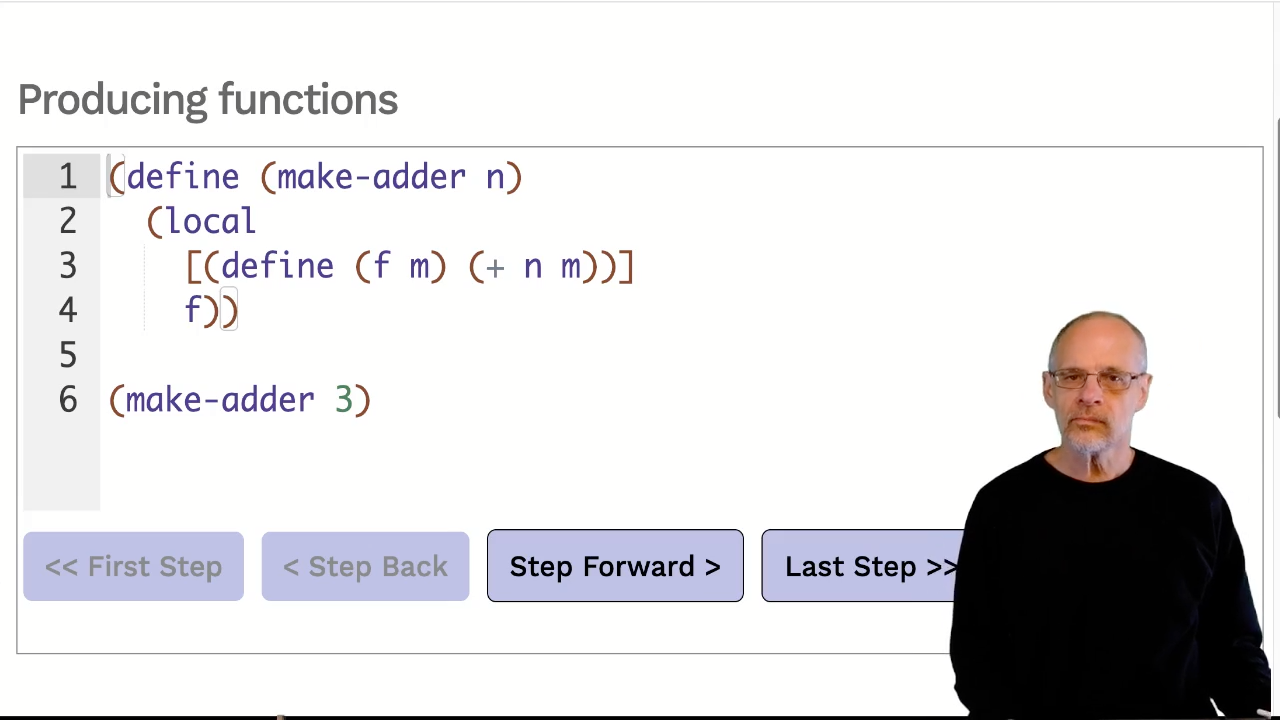
This stepper uses a naming convention that’s hard to reproduce in the slides and commentary. It uses the identifier followed by a small digit. In the slides and commentary, the equivalent is the identifier name, and underscore, and the digit.

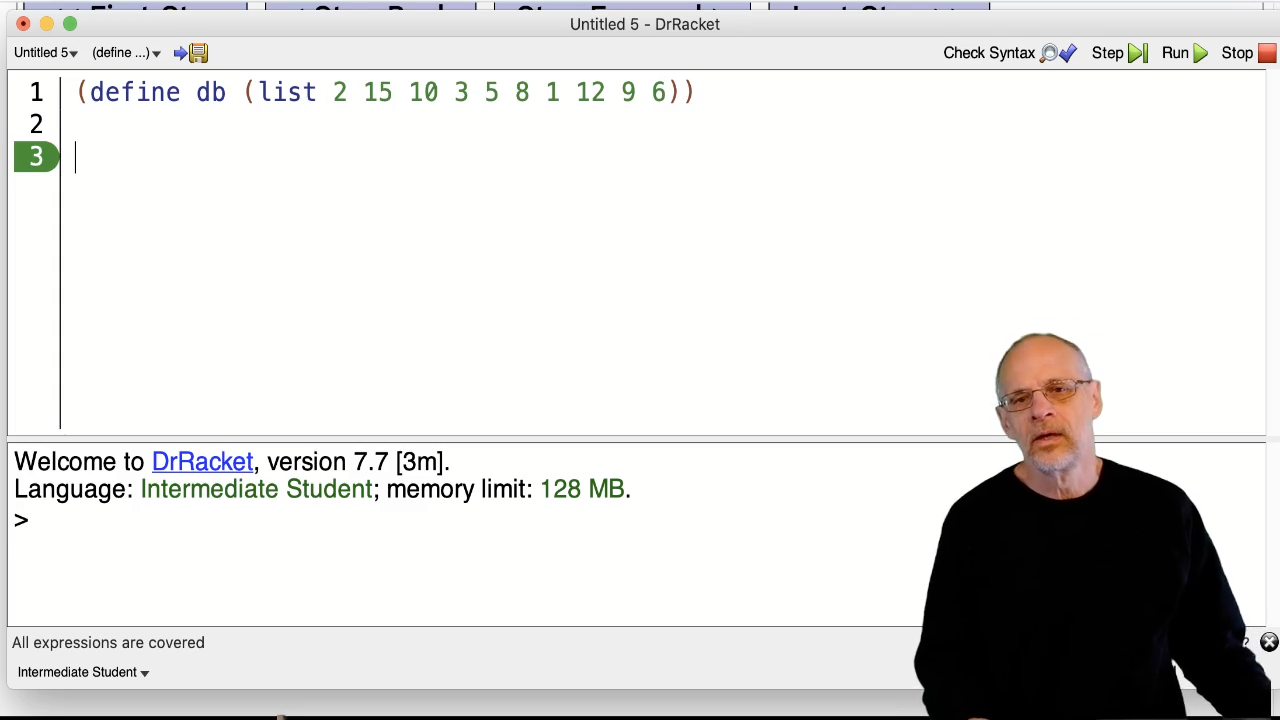
We can bind a value like 3 or "Hello, world!" to an identifier to make a constant. Because functions are values, we can do that with functions, too.

(make-adder 2) produces a function. (define add2 (make-adder 2)) gives that function a name so it can be used over and over.

Is this useful? Why wouldn’t we just define the function directly, like we always have?

Well, here’s a real-world example. scalatags is a Scala library used to generate HTML. Each HTML tag has its own function. Those functions are all pretty similar. Rather than repeat lots of code, the author of scalatags created a function, tag that builds the correct function based on its parameters. Most of the library looks like this:

def tag(s: String, void: Boolean = false): Tag = { ... }
lazy val p = tag("p")
lazy val hr = tag("hr", void = true)
lazy val pre = tag("pre")
lazy val blockquote = tag("blockquote")
lazy val ol = tag("ol")
lazy val ul = tag("ul")
lazy val li = tag("li")

In Racket, it would be something like

;; tag: Str Bool -> function to create a tag
(define (tag s void) (...))
(define p (tag "p" false))
(define hr (tag "hr" true))
(define pre (tag "pre" false))
;; etc

Creating this library without a function-producing-function like tag would likely have a lot more repeated code, more places to fix bugs, involve more typing, etc.

Step through this example. Note that add2 becomes bound to a function. When we get to (add2 3) the identifier add2 is replaced with the thing it’s bound to – just like always.

Functions are first class values. Like other values, they can be:

• Consumed by functions (e.g. filter)
• Produced by functions (e.g. make-adder)
• Bound to identifiers
• Stored in lists and structures (this topic)

Video: Download m15.40_store

In M11 we developed an eval function to evaluate arithmetic expressions. To represent each function, we used a symbol such as '+ and '*. Figuring out which operator to use, based on the symbol, required a bunch of “boilerplate” code – code that is almost, but not quite, the same.

Code in my-apply that is repeated at least once is underlined. There is a lot of it!

Can we do better? Yes.

The key insight is that we’ll store the function itself (it is a first class value, after all!) in the OpNode structure. Notice in the check-expects that make-opnode is consuming +, not '+.

The ??? in OpNode’s data definition is because we don’t (yet) have a way to express a function’s type.

The “observations” are simply recalling what we noted back in M11: (+ ) produces the additive identity (0) and (* ) produces the multiplicative identity (1).

my-apply is now consuming a function rather than a symbol.

In the base case, (op ) produces the identity appropriate to the operator.

In the recursive case, The op function is applied to the first expression on the list of arguments (after it has been evaluated to produce a number) and the result of applying the operator to the rest of the list of arguments (which also produces a number).

Video: Download m15.50_lookup

The motivation for this next section is trying to make the notation for an arithmetic expression easier to read. Here’s a check-expect from the test suite:

(check-expect 
   (eval (make-opnode + 
           (list (make-opnode * (list 4 2)) 
                 3
                 (make-opnode + (list 5 1 2)) 
                 2)))
    21)

Using lists instead of structures allows us to use quote notation (more on this quote notation on the next slide). That makes it look more natural (at least to Racket programmers!):

(check-expect 
   (eval '(+ (* 4 2) 3 (+ 5 1 2) 2)) 21)

You might be wondering why we are doing this. Why do (eval '(+ 1 2 3)) instead of just (+ 1 2 3)?

There are several reasons:

• We may want to read the expression from a file or get it from a user and calculate the result.
• This is a core technology for programs like DrRacket itself.
• Lists can be manipulated and transformed; functions can’t. That’s needed for simplification, differentiation and other Mathcad-like operations on expressions.

More abstractly, we’ve made that expression data rather than code in our program. As data, it’s more flexible. We can process data; we can’t process code in our program.

Items of note:

• Quoting applies to more than lists (which was our motivation). Quoted numbers, strings, and and characters remain unchanged. Quoting is an inherent part of representing symbols.
• Quoting (...) turns the ... into a list.
• Quoting a list of symbols “factors out” the quote to the front of the list.
• Parentheses nested inside a quoted list are also turned into a list. They should not be quoted.
• Because nested parentheses turn into sublists, we cannot (easily) include function applications. Racket turns the function into a symbol (see example 5 on the slide).
• The way we write Boolean values does not work well with quoting; 'true looks like a symbol and is interpreted that way.

Here’s the key idea: make a dictionary (implemented as an association list) mapping symbols to the functions they represent. We can use a slightly modified version of the lookup-al function that consumes a symbol and produces the corresponding function.

Note the double parenthesis in the last line of the slide. That’s a clue that we are now evaluating an expression to obtain the function to use. That is,

((lookup-al '+ trans-table) 3 4 5)
⇒ (+ 3 4 5)
⇒ 12

my-apply in our previous version consumed a function and a list of arguments. my-apply in this version is identical. In eval we use lookup-al to translate a symbol into the function it represents. We pass that function to my-apply.

The other change to eval is to use a list rather than the opnode structure.
As a result, we get the operator with (first ex) and the arguments with (rest ex).

Here’s the code for the examples done in the video. After watching the videos can you repeat the reasoning that leads to the contracts?

;; (make-between n m) produces a function that consumes one number
;;   and produces true if that number is between n and m; false otherwise.
;; Examples:
(check-expect ((make-between 3 5) 2) false)
(check-expect ((make-between 3 5) 3) true)
(check-expect ((make-between 3 5) 6) false)

;; make-between: 
(define (make-between n m)
  (local [(define (f x) (and (<= n x) (<= x m)))] f))



;; (in-discontinuous-range x lof) returns true if x is within the range
;;    of any of the functions in lof.
;; Examples:
(define d-range
  (list (make-between 0 5) (make-between 10 15) (make-between 20 25)))
(check-expect (in-discontinuous-range 4 d-range) true)
(check-expect (in-discontinuous-range 8 d-range) false)

;; in-discontinuous-range: 
(define (in-discontinuous-range x lof)
  (cond [(empty? lof) false]
        [(cons? lof) (or ((first lof) x)
                         (in-discontinuous-range x (rest lof)))]))



;; (make-in-discontinuous-range lof)
;; Examples:
(check-expect ((make-in-discontinuous-range d-range) 4) true)
(check-expect ((make-in-discontinuous-range d-range) 8) false)

;; make-in-discontinuous-range: 
(define (make-in-discontinuous-range lof)
  (local [(define (f x) (in-discontinuous-range x lof))] f))

One of the nifty things that becomes apparent when you look at the contracts (and may not be apparent without the contracts) is that make-between and make-in-discontinuous-range both produce the same type of thing. That means they can be mixed to make new discontinuous ranges:

(define d1 (make-in-discontinuous-range
            (list (make-in-discontinuous-range d-range)
                  (make-between 100 115))))

Cool, eh?

We put the contract in parentheses to keep it distinct from any types it happens to be beside.

Although > has a contract of (Num Num -> Bool), it will also work when the arguments are Ints or Nats. Thus we could also use > as a parameter to a function with the following contract:

function-1: Nat (Nat Nat -> Bool) -> Str

or a function with the contract

function-2: (Int Int -> Bool) -> Sym

but not for a function with the contract

function-3: (Str Sym -> Bool) -> Nat

because > cannot consume arguments of type Str or Sym.

lookup-al is code from just a few slides ago to look up a symbol such as '+ to find the corresponding operator, +. For this to make sense, you need to focus on + and * being binary functions. Ignore that fact that they can be used for a variable number of arguments. In particular, you have to ignore one of our requirements – that the function be defined for zero arguments. Our system for specifying contracts doesn’t handle such functions very well.

A type variable is simply a symbol that stands for some specific, but currently unknown, type. We’ve been using type variables since Module 05 for lists. For example, (listof X).

The difference is now that same variable is going to appear multiple times in the same contract.

Working out the contract using the same style of analysis as the video:

;; (filter pred? lst) keeps all the items on lst that satisfy pred?.
;; Examples:
(check-expect (my-filter even? (list 1 2 3 4 5)) (list 2 4))
(check-expect (my-filter string-upper-case? (list "ABC" "def" "HIG"))
              (list "ABC" "HIG"))

;; my-filter:  (X -> Bool) (listof X) -> (listof X)
(define (my-filter pred? lst)
  (cond [(empty? lst) empty]
        [(pred? (first lst))
         (cons (first lst) (my-filter pred? (rest lst)))]
        [else (my-filter pred? (rest lst))]))

A contract has an arrow, one slot on the right, and a slot on the left for each parameter: ______ ______ -> ______

The examples and the application of empty?, first and rest to lst all suggest that the 2nd parameter is a list: ______ (listof ___) -> ______.

The examples, the result in the base case (empty), and the result in the 2nd clause of the cond (a cons), all suggest that the result is a list: ______ (listof ___) -> (listof ___).

The examples and the way pred? is applied to an argument in the second clause of the cond both suggest that pred? is a function with one parameter: (______ -> ______) (listof ___) -> (listof ___).

The examples and that the result is used to answer the “question” part of the cond clause suggest that pred? produces a Boolean value:
(______ -> Bool) (listof ___) -> (listof ___).

So, what kind of data is in lst? It’s a list of what? Well, look how items on the list are used. The first thing is given to pred? and consd onto the recursive call. There is nothing like <= to suggest a number or symbol=? to suggest that the list contains symbols. We don’t use first or rest on it to suggest that lst is actually a list of lists.

This lack of type-specific operations in the code plus the examples using both integers and strings strongly suggests that it doesn’t matter what kind of data lst contains. So represent that data with a type variable, X: (______ -> Bool) (listof X) -> (listof ___).

The elements of lst, which we’ve assigned the type X are consumed by pred?: (X -> Bool) (listof X) -> (listof ___).

The only elements that are added to the result are items that come from lst. There is nothing that operates on them that might transform them into another type, so we conclude that the result is also a (listof X): (X -> Bool) (listof X) -> (listof X).

One criticism of this approach is that it uses the function’s code but the design recipe suggests writing the contract before writing the code.

Writing the contract first remains good advice. As the slide shows, most if not all of the contract can be derived without looking at the code. Ideally, the contract serves as a guide to writing the code. It’s only in cases where we’re trying to reverse engineer the contract and already have the code available, that we use the code as a guide to writing the contract.