M16: Functional Abstraction

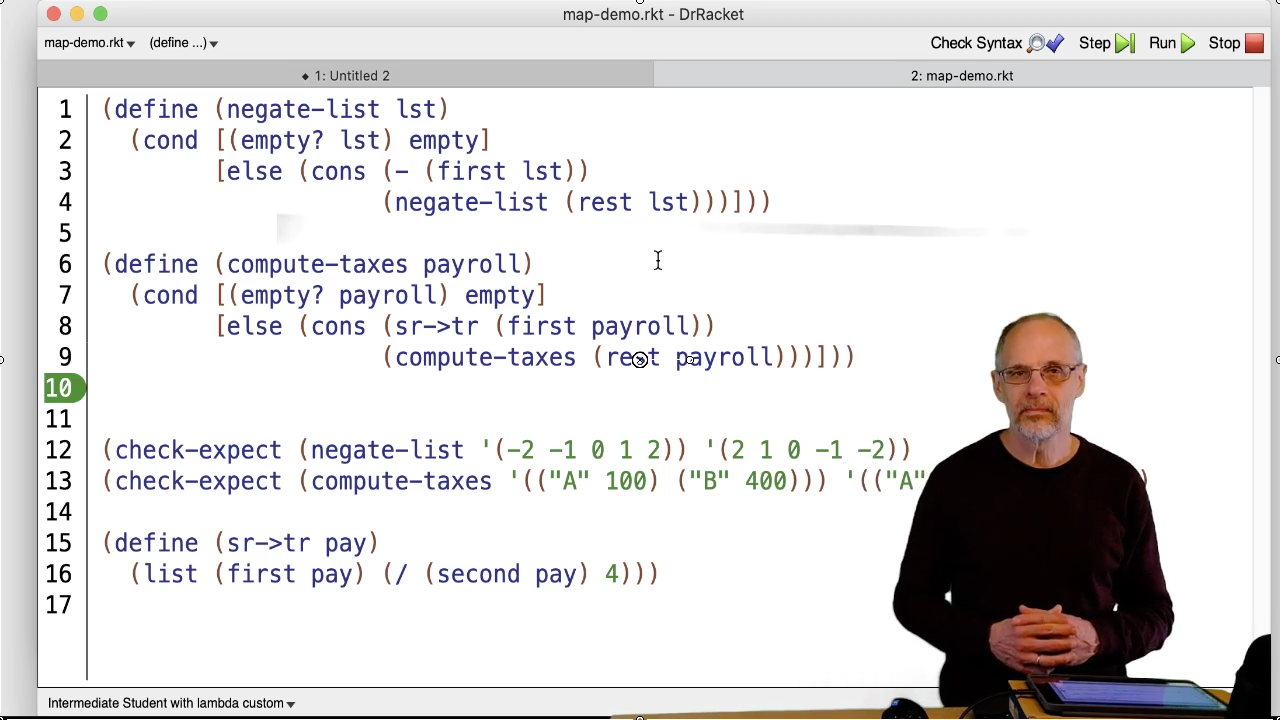
Take negate-list and compute-tax. Rename the function as my-map and rename the pay parameter as lst. The results are identical except for the function applied to (first lst).

Make that function a parameter.

That is, the underlined portions of my-map are all the changes required to account for the differences between negate-list and compute-taxes, other than renaming parameters.

my-map bears a lot of similarity to the listof-X-template. They are based on the same data definition, after all.

(define (listof-X-template lox)
  (cond [(empty? lox) (...)]
        [else         (... (first lox)
                           (listof-X-template (rest lox)))]))

The template, is more general and so leaves out some things that map includes. But both check for the empty list. Both recurse on the rest of the list. Both do something to the first thing on the list.

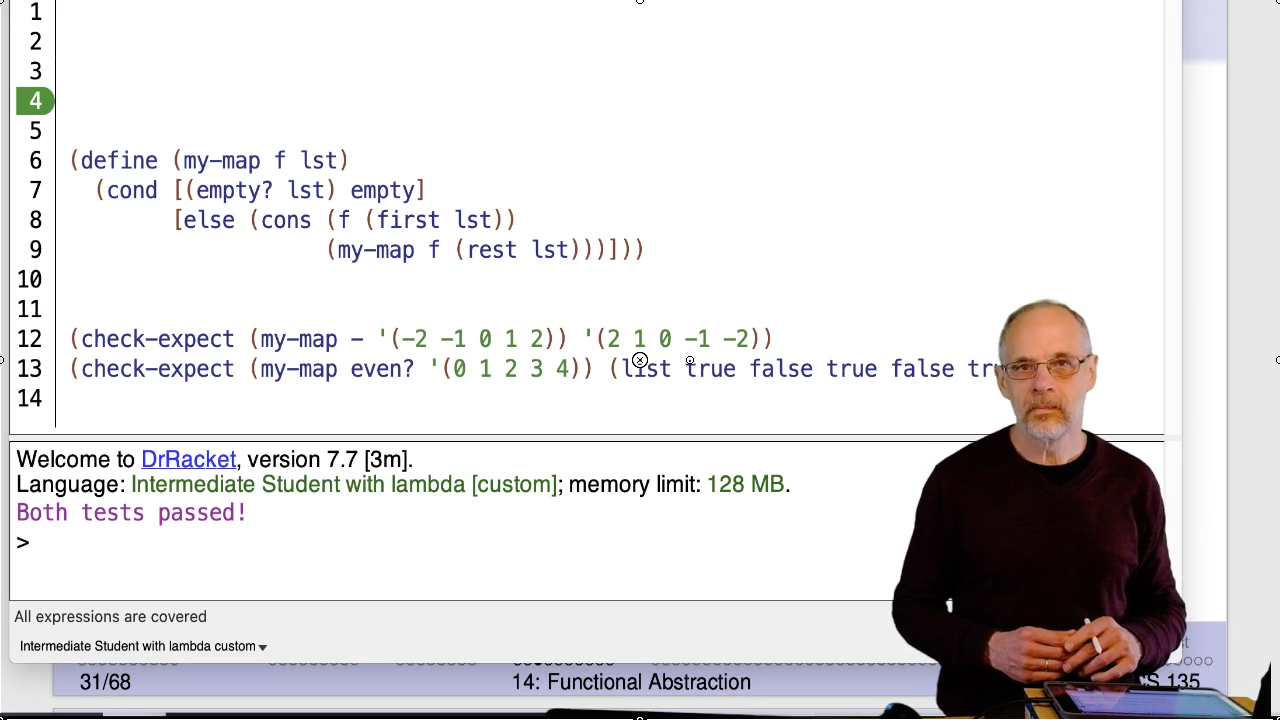
As noted on the slide, Racket provides many built-in higher order functions. CS135 will discuss five of them: filter, map, foldr, foldl, and build-list. These are the only higher order functions you need for CS135. Feel free (but not obligated) to explore the rest, but don’t use them on assignments or exams unless we explicitly point you to them.

One difference between my-map and the built-in map is that the built-in version can consume multiple lists. The function it consumes must have the same number of parameters as there are lists. For example,

(map < (list 5 10 20) (list 3 12 18)) ⇒ (list false true false)

(Note: CS135 used to use the term “Abstract List Function” or “ALF” where we now use “Higher Order Function” or “HOF”. This video still uses the older vocabulary.)

Video: Download m16.50_foldr

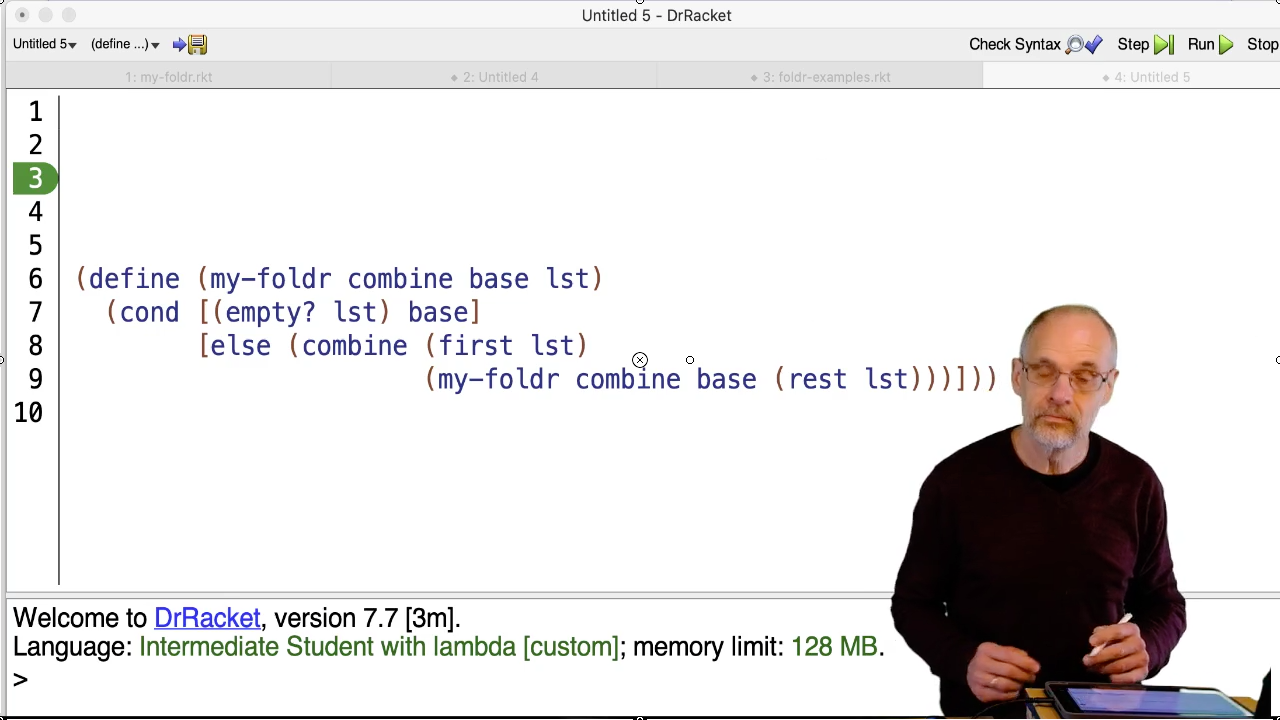
As we did for my-map, let’s harmonize the identifiers we have control over – the function names and parameters – and use underlines to show where the differences are. That gives us this:

(define (my-foldr lst)
  (cond [(empty? lst) ____]
        [else        (____ (first lst)
                           (my-foldr (rest lst)))])
)

This suggests that we need to pass two arguments to my-foldr – one to go into the first blank and one to go into the second.

combine: a function that combines two values, the first thing on the list and the result of processing the rest of the list.

base: a value to provide when we hit the base case.

The contract for foldr is the most complicated contract in CS135.

Video: Download m16.60_foldr_contract

If we were to trace sum-of-numbers, the trace would be pretty short. foldr is built-in. Like other built-in functions, its application results in a single step.

(sum-of-numbers (list 1 2 3 4))
⇒ (foldr + 0 (list 1 2 3 4))
⇒ 10

Note that count-symbols does not use (first lst). Does that “break” foldr?

You may notice that many of our examples use rror as the name of the second parameter of the lambda expression. That’s to remind us which parameter is which. In this case, x is the first value on the list and rror is the Result of Recursing On the Rest of the list (the part that follows x).

Here’s the code for negate-list and one of the functions we used to derive foldr:

(define (negate-list   lst)
  (cond [(empty? lst) empty]
        [else         (cons (- (first lst)) 
                            (negate-list (rest lst)))]))

define (sum-of-numbers lst)
  (cond [(empty? lst) 0]
        [else         (+ (first lst) 
                         (sum-of-numbers (rest lst)))]))

Notice the similar structure! We could have used negate-list as one of our examples to derive foldr. The combining function for negate-list, however, is a bit more complicated. See the explanation on the slide.

We’ll start to use the terminology not explicitly recursive to mean a function where recursion is done via a higher order function such as foldr.

Implementing my-filter using foldr takes a bit more work.

One approach (presented here) is to try to make this code match the structure of foldr so we can identify the values to pass to foldr as the base and combining function. Another approach (the video) is to construct the needed pieces from what we know about the problem and the contracts for my-filter and foldr.

Here’s the code for my-filter. Unfortunately, it does not look much like the code for foldr.

(define (my-filter pred? lst)
  (cond [(empty? lst) empty]
        [(pred? (first lst))
         (cons (first lst) (my-filter pred? (rest lst)))]
        [else (my-filter pred? (rest lst))]))

(define (my-foldr combine base lst)
  (cond [(empty? lst) base]
        [else (combine (first lst)
                       (my-foldr combine base (rest lst)))]))

To make these two functions have the same structure, we can start by moving the last two question/answer clauses into an else clause:

(define (my-filter pred? lst)
  (cond [(empty? lst) empty]
        [else (cond [(pred? (first lst))
                     (cons (first lst) (my-filter pred? (rest lst)))]
                    [else              (my-filter pred? (rest lst))])]))

Next, make the contents of the else clause into a function:

(define (my-filter pred? lst)
  (local [(define (maybe-cons x filtered)
            (cond [(pred? x) (cons x filtered)]
                  [else filtered]))]
    (cond [(empty? lst) empty]
          [else (maybe-cons (first lst)
                            (my-filter pred? (rest lst)))])))

The last three lines of this code matches foldr. It now becomes clear that we could use foldr by passing empty to base and the function maybe-cons to the combining function. Furthermore, we see that maybe-cons is a function that’s only used once and can therefore be replaced with a lambda expression. That results in the following implementation using foldr:

(define (my-filter pred? lst)
  (foldr (lambda (x filtered)
           (cond [(pred? x) (cons x filtered)]
                 [else filtered]))
         empty lst))

An alternative approach to developing this is given in the video.

Video: Download m16.70_filter

In spite of the comment about how higher order functions should be used, we do ask some “brain-bendy” questions to get you to think deeply about how they work.

Harmonizing names, as we did before, results in the following:

(define (my-foldl lst0)
  (local [(define (foldl/acc lst acc)
            (cond [(empty? lst) acc]
                  [else (foldl/acc (rest lst)
                                   (____ (first lst) acc))]))]
    (my-foldl/acc lst0 ____)))

This suggests that we need two additional parameters.

Note the similarity to foldr:

• Both consume a combining function.
• Both consume a base value.
• Both consume a list.

Intuitively, the effect of the application (foldl f b (list x_1 ... x_n-1 x_n)) is to compute the value of the expression (f x_n (f x_n-1 (... (f x_1 b)))).

We can see that by doing a trace, similar to slide 16 :

(my-foldl f 0 (list 3 6 5))
⇒ (foldl/acc (list 3 6 5) 0)
⇒ (foldl/acc (list 6 5) (f 3 0))
⇒ (foldl/acc (list 5) (f 6 (f 3 0)))
⇒ (foldl/acc (list ) (f 5 (f 6 (f 3 0))))
⇒ (f 5 (f 6 (f 3 0)))

foldr and foldl may give the same results; they may be different. For example,

(foldr + 0 (list 1 2 3 4)) ⇒ 10
(foldl + 0 (list 1 2 3 4)) ⇒ 10

but

(foldr string-append "2B" (list "To" "Be" "Or" "Not")) 
⇒ "ToBeOrNot2B"
(foldl string-append "2B" (list "To" "Be" "Or" "Not")) 
⇒ "NotOrBeTo2B"

In general, if the combining operation is commutative foldr and foldl will generate the same result. In these examples, + is commutative but string-append is not.

Aside:

This section is for those who are interested; it is not official CS135 content.

The previous discussion may make you think that in many circumstances the choice between foldr and foldl doesn’t matter. Here is another consideration.

Consider tracing foldr and foldl:

(foldr + 0 (list 1 2 3 4))
⇒ (+ 1 (foldr (list 2 3 4)))  ; omitting + and 0, since they don't change
⇒ (+ 1 (+ 2 (foldr (list 3 4))))
⇒ (+ 1 (+ 2 (+ 3 (foldr (list 4)))))
⇒ (+ 1 (+ 2 (+ 3 (+ 4 foldr empty))))
⇒ (+ 1 (+ 2 (+ 3 (+ 4 0))) ⇒* 10

(foldl + 0 (list 1 2 3 4))
⇒ (f/acc (list 1 2 3 4) 0)
⇒ (f/acc (list 2 3 4) 1)
⇒ (f/acc (list 3 4) 3)
⇒ (f/acc (list 4) 6)
⇒ (f/acc empty 10) ⇒* 10

Notice that the longest step for foldr has as many applications of + as there are numbers in the original list. If we were summing a list with 1,000 numbers, the longest step would have 1,000 pending applications.

Each of those pending applications consumes memory in the computer. If there are too many of them, the computer may run out of memory and be unable to execute the program.

The trace for foldl, on the other hand, never gets longer than a single application of f/acc. Even if the original list had 1,000 numbers, the number of pending applications does not grow and thus does not consume additional memory.

This is an example of tail recursion. Tail recursion is a good thing because it allows for computations to be more thoroughly optimized, especially in terms of the memory consumed by the computation but also in terms of the time it takes.

What is the contract for foldl?

It’s a contract, so it will look like ______ ______ ______ -> ______.

From the trace we did earlier,

(foldl f b (list x_1 ... x_n-1 x_n))
⇒ (f x_n (f x_n-1 (... (f x_1 b))))

we can see that the third parameter is a list of something, say X. Furthermore, we can see from the trace that the combining function consumes two parameters, the first one being an X from the list:

(X ___ -> ___) _____ (listof X) -> _____

The combining function, f, consumes both b and the result of f for its second parameter, suggesting all three of these are the same type. There is no indication that it must be an X so we’ll introduce Y as a new type.

(X Y -> Y) Y (listof X) -> _____

Finally, the result of foldl is the same as the result of the combining function, giving a final contract that is the same as foldr:

(X Y -> Y) Y (listof X) -> Y

Like map, foldr and foldl can handle multiple lists provided the combining function has one parameter for each list plus the “rror” parameter.
For example,

(foldr + 0 (list 1 2 3) (list 4 5 6)) 
⇒ 21
(foldr (lambda (x y rror)
         (cons (+ x y) rror))
       empty (list 1 2 3) (list 4 5 6))
⇒ (list 5 7 9)
(foldl (lambda (x y z rror)
         (cons (+ x y z) rror))
       empty (list 1 2 3) (list 4 5 6) (list 7 8 9))
⇒ (list 18 15 12)

What’s the contract for my-build-list?

We see from examples and the code that it consumes two parameters. The second is a function consuming one argument. We also see from the example and the presence of cons and empty that it produces a list. That gives a partial contract of:

____ (____ -> ____) -> (listof X)

The i in list-from starts at 0 and is only incremented by 1, making it a Nat. The only use of n is comparing to that Nat, so it may as well be a Nat as well. The combining function, f, consumes i (a Nat). Whatever f produces is what goes into the list, which we already designated with X.

That gives a final contract of Nat (Nat -> X) -> (listof X).

foldr and build-list are both built in, so we don’t trace them.

We split the summation into two parts, each handled by a higher order function. The first part is a list of f applied to each of the numbers in 0..n-1; that’s handled by build-list. The second part is summing them up; that’s handled by foldr.