M18: Graphs

In a directed graph each edge has a direction (indicated by the head of each arrow). In an undirected graph, edges do not have directions. This module is concerned exclusively with directed graphs.

What kinds of things are modelled with directed graphs? The water pipes in a city. Airline routes. Routes in Google Maps. Social networks of who follows who. Dependencies such as which functions in a program use which other functions or which subtasks must be completed before a specified subtask is begun.

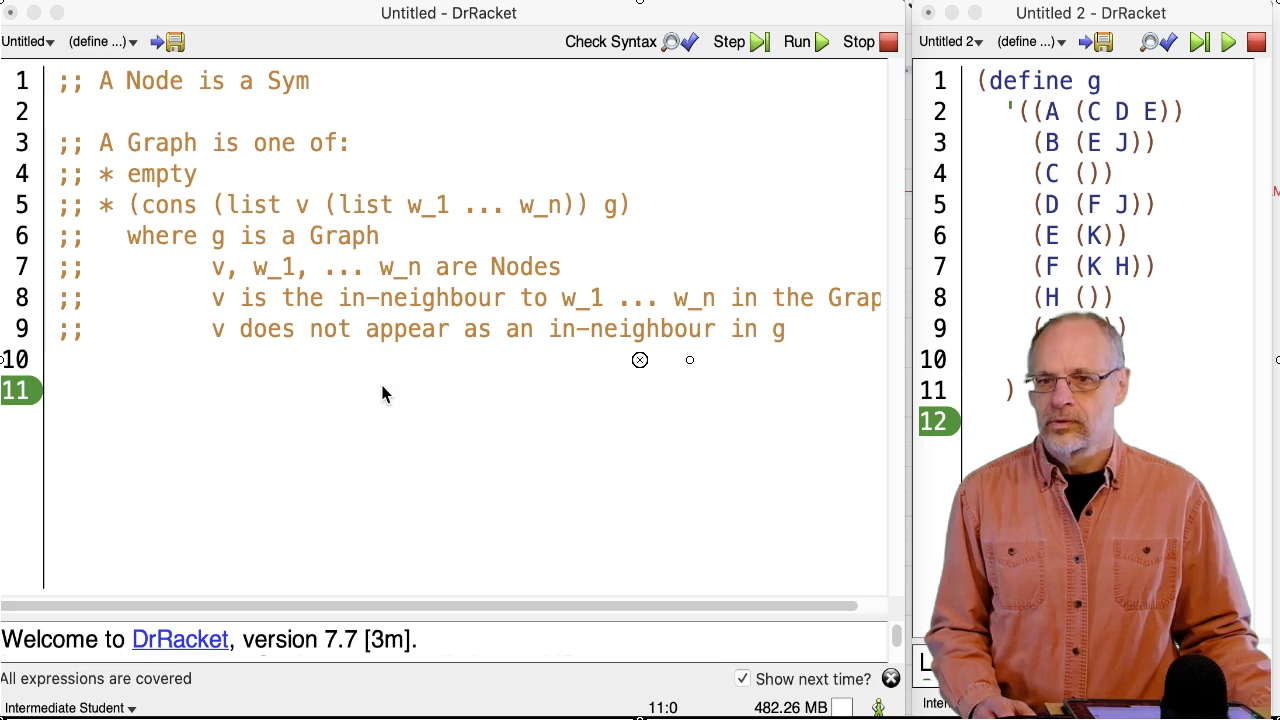
An edge (v, w) is drawn with an arrow from v to w. For example, (A, C) is an edge in the sample graph but (C, A) is not.

In the sample graph, E has two in-neighbours (A and B) and one out-neighbour (K). One path in the graph is coloured. It is the sequence of nodes (A, D, F, H).

This particular graph does not have any cycles. However, adding an edge from J to A would be one of many ways to create a cycle. A cycle is simply a path that allows you to go in circles.

The following self-check questions are with reference to the sample graph shown on the slide.

An adjacency list is a common graph representation, but there are others. They include an “adjacency matrix”, a list of vertices together with a list of edges, etc.

Quoted list notation was discussed briefly as a really compact list notation. There were some details in M14 as part of the general arithmetic expressions example.

Some things to notice about this data definition:

• A Graph is a (listof X) where X is a two element list (a “pair”): (list v (list w_1 ... w_n)). Each pair contains a node name (a symbol) and a list of out-neighbours (a list of symbols).
• The order of the pairs does not matter. The order of the list of symbols (the second element in the pair) does not matter. The order of the node and its associated out-neighbours in a pair does matter.
• We often put the lists of nodes in alphabetical order, but that’s just a convenience.
• The last requirement is just making sure that each node, v, is only listed once in the list of nodes.

A list of two element lists is how we represented an association list, which is a dictionary. We could also represent a graph with other kinds of dictionaries, such as a binary search tree. The keys are the in-neighbours; the values are the lists of associated out-neighbours.

Video: Download m18.30_graph-template

The use of (first (first g)) and (second (first g)) in the template and the neighbours function (next slide) is kind of gross. We might consider replacing them with short, one-liners:

;; (node g) produces the first node from g.
(define (node g) (first (first g)))
;; (adj-nodes g) produces the nodes adjacent 
;;   to the first node in g.
(define (adj-nodes g) (second (first g)))

The code that will be using neighbours is going to assume that the provided node is in the graph. That’s reflected in the requires statement. In addition to that, we’re programming defensively and producing an error if the requirement fails.

We can use higher order functions to implement neighbours:

(define (neighbours-v1 v g)
  (local [(define match-v
            (filter (lambda (x) (symbol=? v (first x))) g))]
    (cond [(empty? match-v) false]
          [else (second (first match-v))])))

Or, if we forgo the defensive programming:

(define (neighbours-v2 v g)
  (second (first (filter (lambda (x) (symbol=? v (first x))) g))))

However, it’s not clear that either of these are improvements.

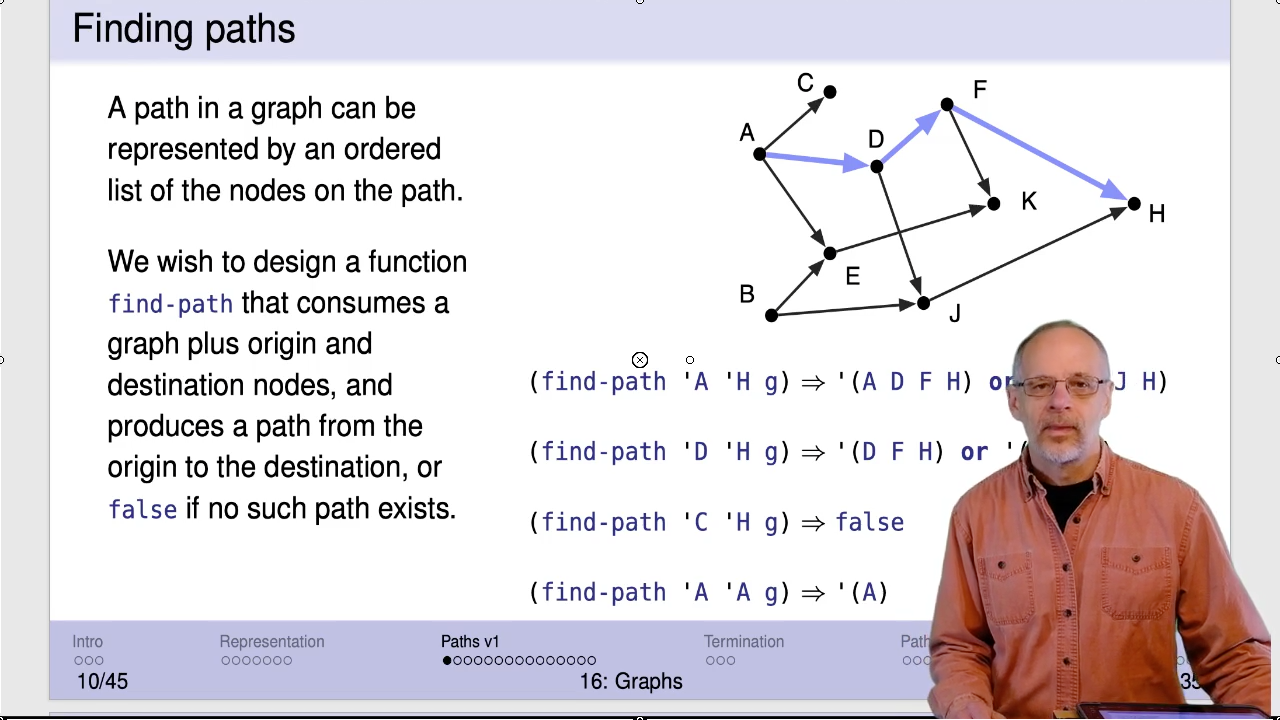
We will develop three versions of find-path. The first version might not terminate on a graph containing cycles. The second version will terminate on all directed graphs but will be very inefficient for some graphs. The third version will be more efficient.

Video: Download m18.40_find-path-v1

Why is generative recursion necessary for find-path? It’s because the first step in our journey along the path is to one of the origin’s neighbours. Those neighbours are generated by applying the neighbours function, not the result of getting one step closer to the base case in the data definition.

This isn’t the first time we’ve seen a backtracking algorithm. search-bt-path (slide 22, Module 10 ) searches for a path in the left side of a binary (sub)tree. If it doesn’t find it, it “backs up” and searches the right side of the binary (sub)tree.

Video: Download m18.60_implicit-graphs

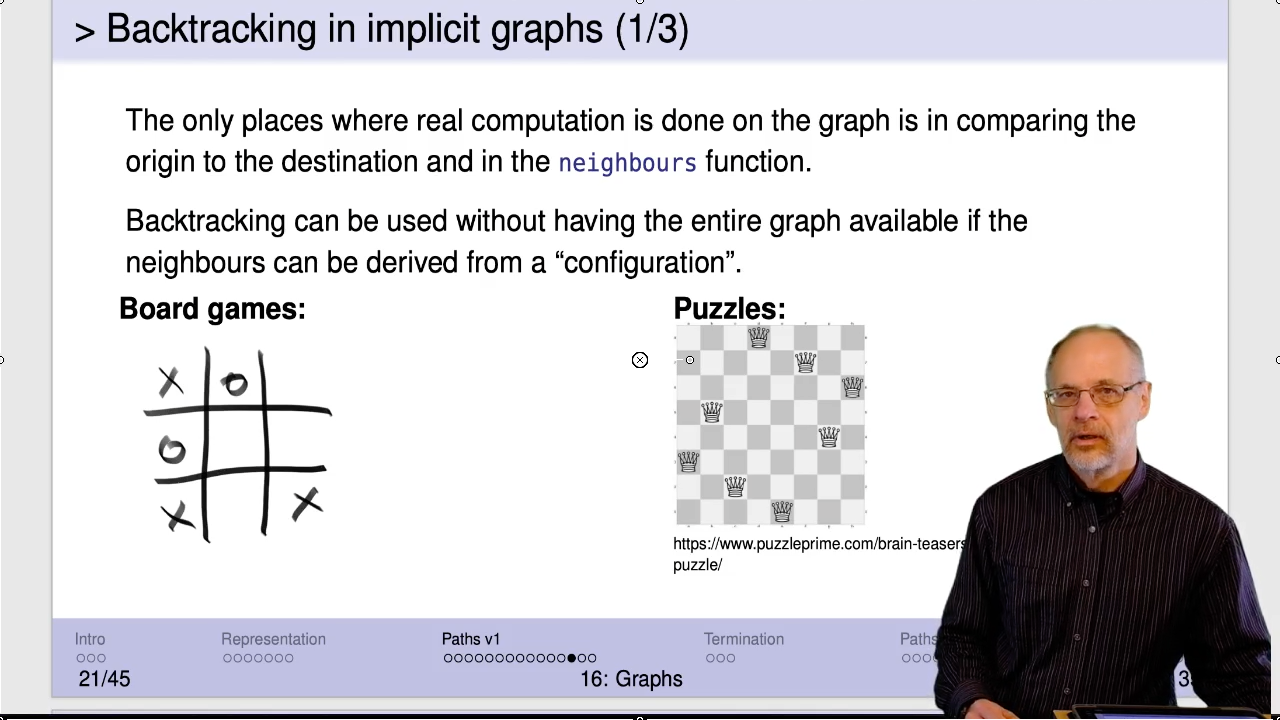
Check out the Sudoku solver .

Note that the tic-tac-toe diagram in the video and on the next slide contains an error. In the second row, the left-most configuration has an “O” in the centre. In the third row, the second configuration has replaced that “O” with an “X”.

The slide’s comment on the graph being acyclic will become more clear in just a few slides when we talk about termination. Briefly, find-path will always terminate on an acyclic graph but will not necessarily terminate on a graph with cycles.

You can play with the Sudoku solver demonstrated in the video to see backtracking in action.

This slide is explaining why find-path will always terminate on a directed acyclic graph. Essentially, once a node is considered as the origin, that node will not be considered again (otherwise there would be a cycle). So the problem is smaller. It keeps getting smaller until either you find a path or there are no nodes left and you know there’s no path.

An application of find-path to a graph with cycles will often terminate. For example, (find-path 'A 'C g) terminates just fine. The problem is that termination is not guaranteed.

With a cycle, (find-path 'A 'D g) eventually calls (find-path 'A 'D g) again. The algorithm has no memory of having previously searched for a path starting with 'A – so it does it again. And again. And again.

Finding a path in a graph is like finding a path out of a maze. find-path needs to use the old trick of dropping breadcrumbs so it knows where in the “maze” it has been before. That will be our second version of find-path.

The underlined parts of the code is what has changed.

There is a new parameter, visited, which accumulates the nodes that have been visited so far. Those are the breadcrumbs referenced earlier.

If find-path/list comes to a neighbouring node that we’ve already visited, we simply skip it and go on to the next neighbour on the list.

find-path/acc is just like find-path in the first version of the algorithm except for the underlined parts:

• Adding the visited parameter to accumulate the nodes visited so far.
• Providing visited, updated to include the current origin, to the accumulator for find-path/list.

Because we’re now using an accumulator that the user of find-path should not need to worry about, we provide a wrapper function with the original name.

Even though we’re using an accumulator, we would not describe find-path as primarily using the accumulative recursion pattern. The fact that it generates parameters for the next recursive application “trumps” the accumulator, making this generative recursion that happens to also use an accumulator.

This is the same example used earlier. We’ll trace the revised algorithm just to make sure we haven’t broken anything that used to work (something called “regression testing”). Then we’ll see if it works on a graph with cycles.

This is the same trace as before except that it’s been augmented to include the accumulator.

As noted, the accumulator is always the reverse of the path from the original origin ('A) to the current node. Therefore, if/when we find the destination node, we could simply reverse the accumulator and produce that as the answer.

If there are an exponential number of paths and find-path explores each of them, the time required to run this function “blows up” like the bad version of max-list.

Video: Download m18.80_find-path-v3

'Z is disconnected from the rest of the graph. To ensure that there is no path from 'D1 to 'Z, find-path-v2 must search every path. It will produce false in the end.

Because all of the paths are explored, the running time of find-path-v2 grows very quickly. In the video, (find-path 'D1 'Z (make-diamond-graph 15)) takes 7.2 seconds while adding only one more diamond increases the running time to 15.4 seconds.

It is possible to get exponential blowup even if 'Z is reachable. Consider having the neighbours of 'D1 be (list 'D1a 'D1b 'Z).

We added an accumulator to keep track of all the nodes we’ve visited and not revisit any that are on the list. So why are we revisiting nodes?

The accumulator is forgetful when find-path backtracks.

The solution to that forgetful accumulator is to explicitly produce its contents when find-path backtracks. But how do we distinguish failure (which produces a list of the visited nodes) from success (which produces a list of nodes on the path)?

In the video, the new version of find-path finds a path in a 160-diamond graph in 1.4 seconds. Recall that the previous version took 15.4 seconds for a graph with 1/10^th the number of diamonds.