M19: Computing History

This module alludes to a lot of advanced material. It might be wise to glance at the goals for this module sooner rather than later.

Cuneiform tablets represent the earliest form of writing that has survived. The writing was pressed into clay and baked, contributing to their longevity. They come from the Babylonian civilization between the Tigris and Euphrates rivers in what is now Iraq.

Many of the surviving tablets represent the record of early computations: treasury inventories, expenditures, business complaints , and tax records. This is another reason for starting the course off with a tax computation.

The New Oxford English Dictionary is a massive dictionary (with Waterloo connections !) that records written passages illustrating the use of each word through time. The first definition of “computer”, with a citation from 1613, is “a person who makes calculations or computations…”.

Euclid’s algorithm for GCD, seen in CS135 and Math135, may be the earliest nontrivial algorithm recorded. But the word “algorithm” comes from Al-Khwarizmi’s name, and the word “algebra” comes from the title of one of his books.

Though Newton’s work is foundational in mathematics, much of Principia Mathematica is explicitly computational; the fourth citation in the OED refers to Newton hiring a human “computer” to help him in his work.

A number of black women “computers” (including Katherine Johnson) were instrumental in the space race. This is portrayed in the 2016 film Hidden Figures .

The Difference Engine was a proof-of-concept for the British Navy, a machine to tabulate polynomials using the difference method (which involves only addition and subtraction). The Navy needed tables of logarithms or trig functions to help with navigation and ballistics. They wanted them mechanically produced to reduce transcription and calculation errors made by human “computers”.

The manufacturing technology of the time wasn’t able to make the parts with the precision and quantity required cheaply enough to make the project feasible.

The Analytical Engine, designed for general-purpose computation, was “programmed” by a series of punched cards (an idea taken from the Jacquard loom, a model of which can be seen in the Ontario Science Centre).

A working implementation of Difference Engine No. 2 was finally completed in 2002, 153 years after it was designed. It was built faithfully to the original drawings and consists of 8,000 parts, weighs five tons, and measures 11 feet long. It was built by and on display at the Science Museum in London, England .

There is a short video of the reconstructed Difference Engine in operation . If your time is limited, start at about 3:20. There is also a Lego implementation , including a video .

She was the daughter of the poet Lord Byron and the wife of the Count of Lovelace, hence an aristocrat by both birth and marriage. Mathematically talented, she was tutored by Augustus de Morgan (the “de Morgan’s laws” guy).

She is sometimes called the first programmer, because one of her articles describes the implementation of an algorithm for the Analytical Engine, but “first computer scientist” is more apt because of the importance she placed on communication and conceptual understanding.

She died young of uterine cancer; Babbage died old and embittered, his plans never having had succeeded during his lifetime.

So… who cuts the barber’s hair?

This is an example of a proposition that references itself. We’ll run into several more in this lecture module.

Video: Download m19.20_hilbert

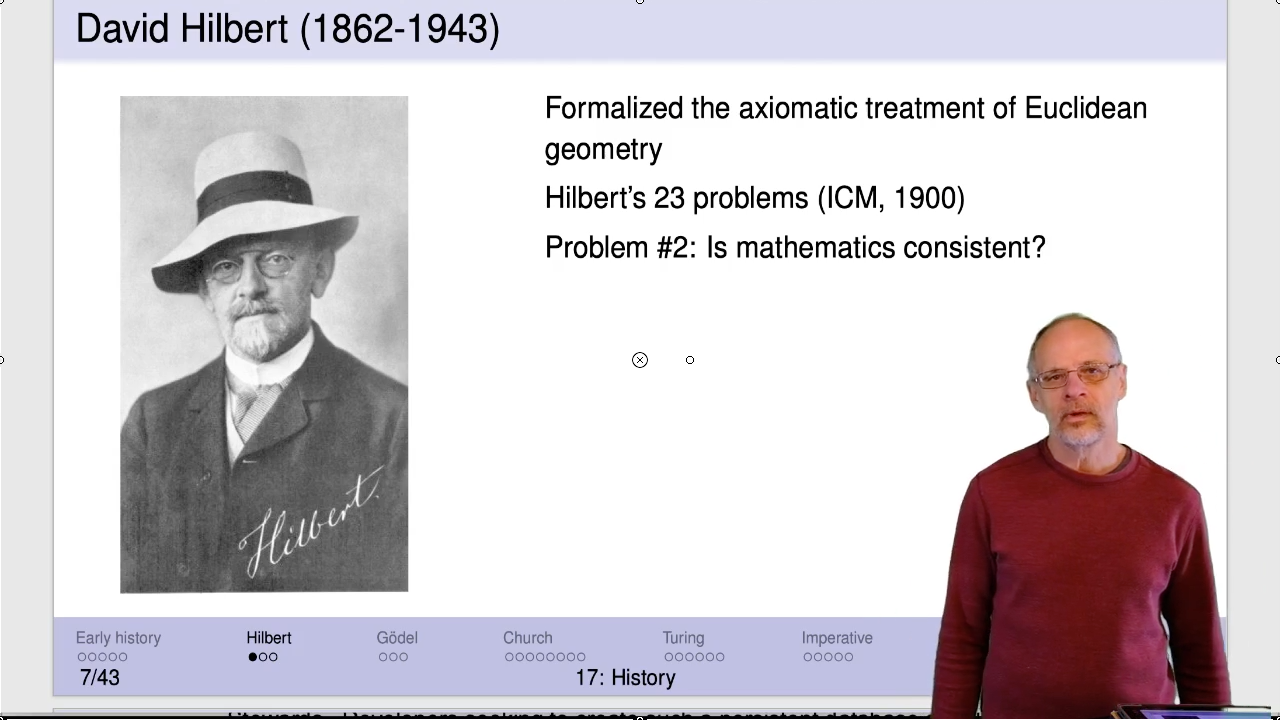
Hilbert’s 23 problems were collected for the keynote address at the 1900 International Congress of Mathematicians. The most recent one to be solved (the undecidability of general Diophantine equations) was solved in 1970. A number of these remain unsolved.

Work on three of these problems became foundational to computer science. Solving the first two led directly to solving the third using two different approaches. The first approach led to functional programming and the second approach led to modern computer architecture and imperative programming.

The three problems from Hilbert’s list that we want to discuss all have to do with formulas, theorems, and proofs.

The example that’s referenced, that the square of any even number is also even, has a short proof even though it is about an infinite set.

Hilbert’s questions were first framed in his 1900 speech to the International Congress of Mathematicians. But they continued to evolve as people worked on them. By the 1920’s the three we’re interested in were generally framed this way.

Video: Download m19.30_godel

Gödel did the work described here when he was just 25, a year after finishing his doctorate at the University of Vienna. The photograph is taken later in life, when he was a fellow of the Institute for Advanced Studies at Princeton and a confidante of Einstein.

Gödel developed paranoia late in life, and starved himself to death because he was convinced that his food was being poisoned.

The choice of λ (lambda) that has figured prominently in Modules 15 and 16 of CS135 and functional programming in general is an historical accident.

Church was creating a notation to describe functions on natural numbers, so of course he needs to define the numbers. He used a technique pioneered by Georg Cantor, the creator of set theory.

Just in case you want to play in DrRacket:

(define zero  (lambda (f) (lambda (x) x)))
(define one   (lambda (f) (lambda (x) (f x))))
(define two   (lambda (f) (lambda (x) (f (f x)))))
(define three (lambda (f) (lambda (x) (f (f (f x))))))

But how do you use these? Watch the video!

This was the first proof that a particular mathematically definable function was impossible to compute in a general model of computation—and all this before physical computers existed.

The function, f, could be implemented several different ways. For example, it could be a large cond expression:

(define (f s c)
    (cond [(and (symbol=? s 'init) (char= c #\0)) (list 'saw-0 #\space 'R)]
          [(and (symbol=? s 'saw-0) (char= c #\0)) (list 'saw-0 #\0 'R)]
          ...))

Alternatively, we could have a dictionary with a key of state and character:

(define p (list (list (list init #\0) (list 'saw-0 #\space 'R))
                (list (list 'saw-0 #\0) (list 'saw-0 #\0 'R))
            ...))

This dictionary could be provided to f as a parameter and the body of f simply becomes an appropriate lookup function. With this impementation, f is equivalent to the CPU on a modern computer and the dictionary is equivalent to the program.

But separating the control function f and the “program” in this fashion is getting ahead of ourselves. In the subsequent slides the “controller” f refers to a single function as described on the slide. It consumes a state and a character read from the tape. It produces a new state, character to write to the tape, and a head motion.

A working Turing machine (download) in Racket builds on the above ideas. This implementation includes a Turing machine program that determines whether a binary string on the tape is a palindrome.

An excellent write up by UWaterloo’s own Craig Kaplan on this topic is at https://cs.uwaterloo.ca/~csk/halt/ . As of 2022-02-27, Googling “halting problem” lists this site immediately after Wikipedia (not counting Google’s obligatory YouTube videos). It’s held that position since at least December 2012.

It uses the C programming language for exposition rather than Racket, as in the video.

Movies about Alan Turing:

• Breaking the Code (1996)
• Codebreaker (2011)
• The Imitation Game (2014)

The photo is of von Neumann with ENIAC.

von Neumann was probably the greatest mathematician of the twentieth century, making fundamental contributions in a number of areas of mathematics and science (differential geometry, game theory, economics, quantum physics). On a more mundane note, he invented mergesort.

The EDVAC report reads like a high-level description of the parts of a modern computer. In particular, the notion of a stored program (essential in Turing’s proofs) completed the trend started by Babbage by erasing the distinction between specification and execution, or program and data, a notion we have alluded to in CS135 by noticing how closely Racket programs resemble Racket data structures. But the lack of support for recursion (a practical decision; as a mathematician, von Neumann knew of its importance) would have a major impact on the future development of programming languages.

A professor at a New England college when World War II broke out, she volunteered for the Navy and never left it, rising to the rank of rear admiral.

Hopper’s main contribution was in making programs readable and writeable by people without intimate knowledge of a particular machine architecture. The major conference on women in CS is named after her, as is an ACM award to young researchers.

COBOL (COmmon Business-Oriented Language) is verbose enough that a complete program is too long to include here. An example statement:

ADD a, b TO c
    ON SIZE ERROR
        DISPLAY "Error"
END-ADD

COBOL was the principal programming language for business programs running on mainframes for decades. A 2022 survey estimated there are as many as 800 billion (with a B) lines of COBOL code still in production.

The program computes and prints the first ten Fibonacci numbers.

FORTRAN had no support for recursion because the underlying hardware did not, and no data structures beyond arrays. Lists had to be simulated using arrays.

Backus’s proposal in his 1978 Turing award lecture unfortunately went nowhere.

Through the 1970’s, the two CS courses required of all UW Faculty of Math students taught them programming in FORTRAN and COBOL (with COBOL recommended as a first course for those in co-op).

Left photo: McCarthy at MIT.

Right photo: McCarthy at Stanford in later life.

car stands for “contents of address register”, and cdr for “contents of decrement register” – two machine language instructions on the IBM 704 that were used a lot in the Lisp interpreter to access the data and the rest of the list.

Why does Lisp “encourage redefinition and customization of the language”?

Consider the expression trees we worked with in M13. We wrote programs that consumed a list of symbols such as (list '+ 2 (list '* 3 4)) and “interpreted” that to get 14.

It doesn’t take much to add symbolic constants, cond expressions, and function applications – in short, to extend it to a complete language.

Representing a Lisp program (perhaps with some “enhancements” so it’s no longer plain Lisp) in a general tree is easier than with most other languages. Once it’s in a general tree, another Lisp program can interpret or “run” it, just like we did with the arithmetic expression trees.

All this can be done without having to write low-level code as would typically need to be done with most other languages.

An alternative to CS136 is CS116. It covers many of the same computing concepts but using the Python programming language rather than C. Both languages can be used to learn important imperative programming concepts and both are used extensively in the “real world”.

CS116 takes a slower approach than CS136 and Python is more accessible than C. On the other hand, C facilitates understanding what is really happening at the machine level, which is important for computer science students. CS136 is required for before taking 2nd year CS major courses.